Виды электромагнитных волн.

Рассмотрим наиболее простой вид электромагнитных волн - электромагнитные гармонические (монохроматические) волны. Для электромагнитных гармонических волн величины векторов 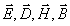изменяются во времени по закону косинуса или синуса. Если какой либо один из четвёрки векторов электромагнитной волны меняется по закону косинуса или синуса, то, как это следует из системы уравнений Максвелла, и другие три вектора будут меняться во времени как функции синуса и косинуса. Итак, изменение вектора напряжённости электрического поля 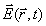электромагнитной гармонической волны определяется следующим выражением:

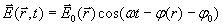(1.2)

где 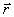- радиус вектор точки наблюдения с координатами 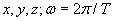- круговая частота колебаний [рад/сек], определённая периодом колебаний 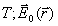- амплитуда колебаний электрического поля, зависящая от положения точки наблюдения. В дальнейшем будем называть полной фазой колебаний волны аргумент функции косинуса в выражении (1.2):

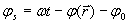
Значение начальной фазы 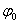колебаний зависит от выбора момента начала отсчёта времени и/или положения центра декартовой системы координат. По этой причине можно считать 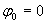. Из выражения (1.2) следует, что полная фаза гармонической волны имеет две составляющие:

а) временную составляющую фазы 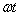, линейно изменяющуюся во времени со скоростью изменения, равной круговой частоте колебаний ;

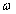б) пространственную составляющую фазы 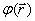, характер зависимости которой от положения точки наблюдения 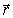, как мы увидим ниже, определяется расстоянием 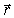, пройденным волной от источника до точки наблюдения, т.е.:

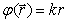, где 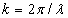- волновое число, определяемое длиной волны 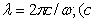- скорость света в вакууме).

Отсюда следует, что пространственная составляющая полной фазы является линейно изменяющейся функцией от расстояния, пройденного волной. Можно определить скорость изменения фазы волны в зависимости от пройденного волной расстояния величиной приращения фазы на расстоянии, равным единице длины ( в системе CИ - 1м). В соответствии с этим определением скорость изменения фазы волны в зависимости от пройденного волной расстояния равна волновому числу 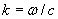. По аналогии с круговой частотой 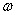волновое число 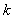называют пространственной частотой. Размерностью волнового числа (пространственной частоты) в системе СИ является м^-1 . В оптике используется внесистемная единица измерения волнового числа, имеющая размерность мм^-1 и называемая 'числом линий на мм' . Физическое содержание такого названия станет понятным ниже в главе 5 при изучении явления интерференции света. Особенностью гармонической электромагнитной волны (1.2) является зависимость полной фазы её колебаний 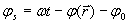, как от времени, так и от положения точки наблюдения в пространстве.Отметим, что периодичность изменения во времени гармонической, электромагнитной волны влечёт за собой в силу (1.1b) периодичность пространственного изменения векторов 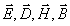. В проявлении этого свойства гармонических электромагнитных мы убедимся далее. Другим свойством электромагнитных волн является характер зависимости от положения точки наблюдения пространственной составляющей полной фазы и связанной с ней амплитуды колебаний четвёрки векторов электромагнитного поля.

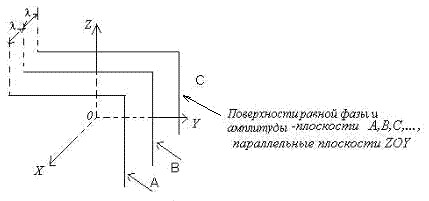
Рис. 1.1.

где 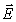0 - амплитуда колебаний электрического вектора, постоянная во всех точках пространства; k x=(( 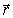) - пространственная составляющая полной фазы волны, которая имеющая постоянное значение в любой плоскости, параллельной плоскости ZOY, определяемое расстоянием, которое прошла

волна от точки 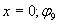- начальная фаза колебаний волны при 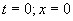. Колебания вектора напряжённости магнитного поля такой волны будет определяться аналогичным Выражением

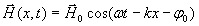(1.3b)

где 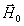- амплитуда колебаний электрического вектора, постоянная во всех точках пространства. Кроме плоских гармонических волн известен достаточно широкий класс электромагнитных волн, у которых амплитуда изменяется с расстоянием. Наиболее простыми из них являются цилиндрические и сферические волны. Представление о цилиндрических волнах можно почерпнуть из наблюдений волн на поверхности воды в водоёме, после того, как в него брошен камень. Амплитуда и фаза колебаний четвёрки векторов цилиндрической волны имеет постоянное значение на концентрических поверхностях (рис.1.2a) вдоль оси симметрии которых расположены источники колебаний. На достаточно большом расстоянии 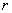точки наблюдения от источника колебаний амплитуда, создаваемой им цилиндрической волны, убывает обратно пропорционально 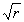(см. задачу 1.1b). Амплитуда и фаза колебаний четвёрки векторов сферической волны имеет постоянное значение на концентрических сферических поверхностях (рис.1.2b), в центре симметрии которых расположены источники колебаний. На достаточно большом расстоянии 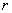точки наблюдения от источника колебаний амплитуда, создаваемой им сферической волны, убывает обратно пропорционально r (см. задачу 1.1a).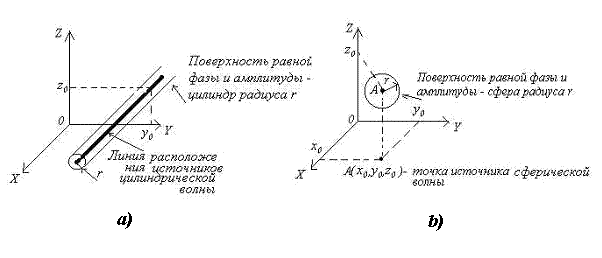

Рис. 1.2.