Дифракция света на щели

Пусть на непрозрачный плоский экран, в котором вырезана длинная узкая щель, падает нормально плоская гармоническая волна

Е=Е₀ cos(ωt + kz + a₀). (13.22)

За экраном помещена собирающая линза, в фокальной плоскости кото­
рой расположен экран для наблюдения дифракционной картины (рис.
13.8). В каждой точке Р на экране собираются вместе и интерферируют
идущие от щели параллельные лучи вторичных волн. На рис. 13.8 по­
казаны такие лучи, образующие угол θ с нормалью к плоскости щели.
Для определения амплитуды суммарного колебания в точке Р применим принцип Гюйгенса - Френеля и принцип суперпозиции. С этой целью за тянем щель плоской поверхностью σ. Эта плоскость удобна тем, что она совпадает с фазовой плоскостью падающей волны. В качестве элеменTов dσ поверхности, являющихся источниками вторичных волн, выберем
узкие полоски, "вырезанные" из поверхности σ вдоль щели. Одна из таких полосок показана на рис. 13.8. Расстояние до края О₁ щели до этой полоски обозначим х. При этом ее ширина будет равна dx. Колебание, возбуждаемое в точке Р вторичной волной, пришедшей от этой полоски, имеет вид:
dE = dE_m cos(wt-k*AP + a_o), (13.23)

где амплитуда dE_m согласно принципу Гюйгенса - Френеля пропорциональна ширине

полоски:

dE_m = С dx , (13.24)

здесь С - коэффициент пропорциональности

Линза обладает свойством таухронизма, которое выражается в том, что оптические длины О₁Р и ВР двух лучей равны. Такие лучи на­зываются таухронными. Это название означает, что свет преодолевает расстояния О₁Р и ВР за одинаковое время. С учетом этого свойства для оптической длины луча АР, идущего от полоски da, можно запи­сать следующее выражение

AP = O₁P+ x sin θ (13.25)

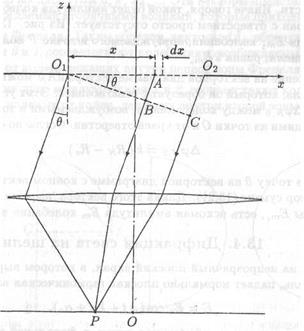
Рис. 13.8. К описанию дифракции Фраунгофера на щели

Подставим выражения (13.24) и (13.25) в формулу (13.23). Следуя прин­ципу суперпозиции, найдем колебание в точке Р, возбуждаемое вторич­ными волнами, идущими от всех элементов поверхности σ:

E(t) = C 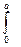cos(ωt - k x sin θ + a_A)dx,

где a = a₀ – k* O₁P, a - ширина щели. Вычислим этот интеграл по

формуле Ньютона - Лейбница:

Е= 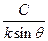( sin(ωt + a_A) - sin(ω t - k a sin θ+a)).

Преобразуем это выражение при помощи тригонометрической формулы (13.10). Получим:

Е = Е_т cos (ω t – (1/2)k a sin θ+a)). (13.26)

где амплитуда колебаний

E_m = E_mo 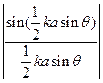(13.27)

Е_то = С а. Согласно этим формулам, в точке О, лежащей против сере­дины щели и соответствующей θ = 0, колебания вектора Епроисходят по закону

Е = Е_то cos(ωt +а). (13.28)

При выводе этой формулы учтено, что при малых значениях аргумента х можно положить sin х ~ х. График зависимости амплитуды Е_т от sin θ представлен на рис. 13.9.

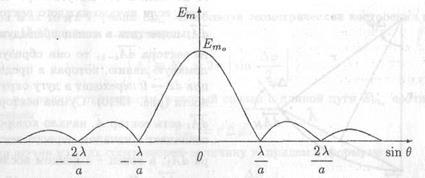
Рис. 13.9. Дифракция Фраунгофера на щели. График зависимости амплитуды Е_т от sin θ

Амплитуда (13.27) обращается в ноль при θ ≠ 0, если

sin((1/2) k a sin θ)=0

Отсюда следует, что

sin θ =2πm/(ka) (13.29)

где т = ±1, ±2,...

Формулу (13.27) для амплитуды светового колебания в произвольной точке Р на дифракционной картине можно получить посредством опи­санного в разделе 13.2 графического метода. Для этого фазовую плос­кость, затягивающую щель, разобьем на узкие полоски одинаковой ши­рины dx. Пусть i = 1,2,..., N - номер полоски. Колебание в точке Р, возбуждаемое волной, пришедшей от произвольной полоски, будет описываться формулой (13.23). Каждое колебание следует представить вектором dA_i, длина которого равна амплитуде dE_m колебания, а угол между этим вектором и некоторым произвольным направлением (осью х) - начальной фазе колебания. Так как все полоски имеют одну и ту же ширину dx, амплитуды колебаний в точке Р, создаваемых вторичными волнами от различных полосок, будут одинаковы. Разность фаз между колебаниями от соседних полосок равна

∆φ = к dx sin θ

и не зависит от номера i полоски. Таким образом, векторы dA_i, представляющие колебания от различных полосок, будут иметь одну и ту же длину dE_m, и каждый вектор будет повернут относительно предыдуще­го на один и тот же угол ∆φ. При этом, если начало каждого вектора

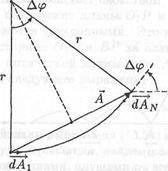
Рис. 13.10. Векторная диаграмма

dA_iпоместить в конец предыдуще­го вектора dA_i-1 , то они образуют ломаную линию, которая в пределе при dx —> 0 переходит в дугу окруж­ности (рис. 13.10). Сумма векторов dA_iесть вектор А, начало которого совпадает с началом первого векто­ра dA₁ , а конец - с концом послед­него dA_N. Как видно из рис. 13.10, длина вектора А равна длине хор­ды, стягивающей дугу окружности из слагаемых векторов dA_i.

Разность фаз ∆φ между колебаниями в точке Р от вторичных волн, приходящих от краев щели О₁ и O₂, определяется разностью длин лучей

О₁P и O₂P (рис. 13.8):

∆φ = k a sin θ . (13.30)

При этом угол между векторами dA₁ и dA_N, представляющими эти ко­лебания, будет равен ∆φ.

В точке О на экране собираются лучи, идущие под углом θ = 0. Все колебания в этой точке имеют одну и ту же фазу (∆φ = 0). Поэтому все

векторы dA_iимеют одно и то же направление, а модуль их суммы будет равен сумме модулей этих векторов (рис. 13.11):

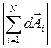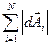= =N dE_m= Е_то

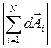
Рис. 13.11. Векторная диаграмма при θ = 0

Так как амплитуды dE_m колебаний практически не зависят от угла θ, длина дуги окружности на рис. 13.10, т.е. сумма

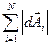
для всех точек Р равна Е_то. Используя геометрические построения на рис. 13.10, найдем длину хорды:

|A|= Е_т =2r sin(∆φ/2)

где r - радиус окружности, который связан с длиной дуги Е_то, соотно­шением

Е_то =r∆φ.

Исключив из этих соотношений величину r, придем к формуле

Е_т = Е_то | sin(∆φ/2)/(∆φ/2) (13.31)

которая после подстановки в нее выражения (13.30) принимает вид (13.27). Учитывая, что интенсивность I ~ Е_m ², нетрудно найти ее за­висимость от θ