Уравнение непрерывности

Выражает локальный характер закона сохранения заряда. Это значит, что заряд не может исчезнуть в одном месте и появиться в другом, но он должен протечь из первого места во второе.

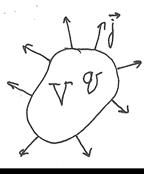
Итак, пусть S – произвольная замкнутая поверхность в проводящей среде, в которой течет ток. За время dt из нее вытекает заряд dq, причем

.

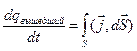Тогда внутри этой поверхности заряд изменится на величину 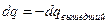. Поэтому

.

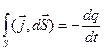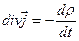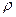Это и есть уравнение непрерывности. В дифференциальной форме оно принимает вид: , где – объемная плотность заряда.

Важное следствие: в случае стационарного тока (плотность тока во всех точках среды не меняется со временем) поток вектора 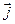через любую замкнутую поверхность равен нулю:

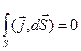, а также .

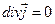Заряд не может накапливаться внутри замкнутой поверхности; сколько линий тока в нее входит, столько же и выходит.