Стационарные токи в однородной проводящей среде
Рассмотрим трубку тока в однородной проводящей среде. Плотность тока j в произвольном нормальном сечении трубки связана с силой тока I и площадью сечения 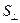 соотношением:
соотношением:
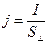 ,
,
причем сила тока одна и та же в любом сечении, если ток стационарный (иначе заряд накапливался бы между двумя сечениями трубки).
 Запишем закон Ома в локальной форме:
Запишем закон Ома в локальной форме:
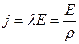 ,
,
или 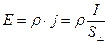 (1).
(1).
Умножим обе части уравнения (1) на элемент длины dl трубки тока и проинтегрируем по всей длине трубки от начального сечения 1 до конечного 2, двигаясь по току, т.е. вдоль линии напряженности:
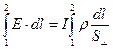 (2).
(2).
Интеграл в левой части уравнения (2) есть разность потенциалов 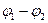 (или напряжение
(или напряжение 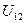 ) между концами 1 и 2, интеграл в правой части, зависящий от формы и размеров трубки и удельного сопротивления среды, называют сопротивлением данного участка трубки – обозначим его
) между концами 1 и 2, интеграл в правой части, зависящий от формы и размеров трубки и удельного сопротивления среды, называют сопротивлением данного участка трубки – обозначим его 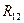 . Итак, мы получаем:
. Итак, мы получаем:
 , или
, или 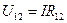 (3),
(3),
где 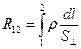 (4).
(4).
Это соотношение называют законом Ома в интегральной форме.
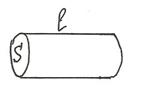
Сопротивление однородного проводника цилиндрической формы, как следует из (4), равно
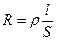 ,
,
где l – длина проводника, S – площадь его нормального сечения.
Единица измерения сопротивления в СИ – 1 Ом. Как видно из закона Ома (3), Ом=В/м.
Дата добавления: 2015-06-12; просмотров: 2591;
