Метод простых итераций

Систему нелинейных уравнений можно записать в виде

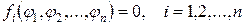(60)

Если неизвестные 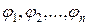и функции 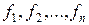рассматривать как n-мерные векторы 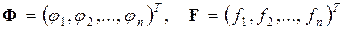, то систему (60) можно записать кратко в векторном виде .

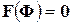Систему исходных уравнений (60) представим в эквивалентном виде, удобном для проведения итераций:

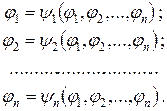(61)

При численном подходе задача о решении нелинейных уравнений разбивается на два этапа: локализация (отделение) корней, т.е. нахождение таких отрезков на осях, в пределах которых содержится один единственный корень, и уточнение корней, т.е. вычисление приближенных значений корней с заданной точностью.

Если известно какое-то приближенное значение решения системы уравнений: 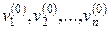, то последующие приближения решения можно вычислить методом простой итерации по алгоритму:

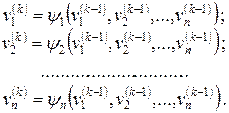(62)

либо методом, для линейных систем алгебраических уравнений, с использованием в текущей итерации ранее вычисленных компонент вектора:

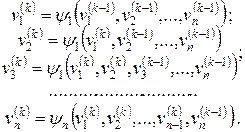k=1,2,…

Итерационный процесс продолжается до выполнения условия сходимости итераций 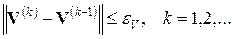, где e_V – малая величина, погрешность решения.

В векторном виде систему уравнений (61) можно записать кратко в виде

,

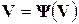а итерационный алгоритм (62) в виде

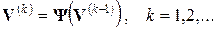
Если данный итерационный процесс сходится, то он сходится к решению системы уравнений.

Для сходимости итерационного процесса необходимо, чтобы норма производной вектор-функции 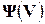была меньше некоторого положительного числа 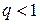в некоторой окрестности 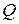области решения системы, из которой не выходят приближенные значения 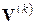при итерации

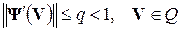. (63)

Следует обратить внимание на способ записи уравнений. Рассмотрим на примере. Пусть задано одно нелинейное уравнение 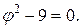Как вы понимаете, точные значения его корней 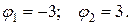В требуемой итерационной форме это уравнение можно записать по-разному:

1.

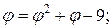
2.

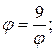
3. 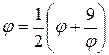и т.п.

Есть ли разница при численном решении? Чтобы ответить на данный вопрос, вычислим производные от правых частей этих выражений в начальной точке :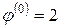

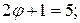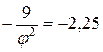1. 2. ; 3.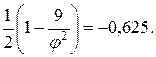

Нормой этой производной является его модуль. Как мы видим, условие сходимости итерационного процесса выполняется только в третьем случае. При приближении к решению 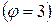норма производной в первом случае только увеличится, т.е. итерационный процесс будет расходящимся. Во втором случае норма производной тоже больше 1, итерационный процесс тоже будет расходящимся. Но можно заметить, что если начальную точку взять больше 3, то норма производной станет меньше 1 и процесс будет сходящимся. Но сходиться он будет медленно, т.к. по мере приближения к решению норма производной будет стремиться к 1. В третьем случае итерационный процесс сходится, причем очень быстро, т.к. при приближении к решению норма производной стремится к 0.

Метод касательных (Метод Ньютона)

Формулы метода Ньютона для систем нелинейных уравнений, как и в случае одного нелинейного уравнения, получаются посредством применения формулы Тейлора для функции 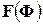в окрестности решения 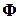. Пусть нам известно некоторое (k-1)-е приближение 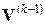к решению 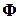системы (60). Поэтому решение можно представить как

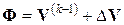(64)

где 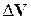– приращение (поправка) к приближенному решению. В развернутом виде это уравнение записывается как

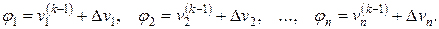
Разложим функцию 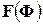в ряд Тейлора по малому параметру 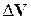, оставив в силу малости параметра только два первых члена разложения:

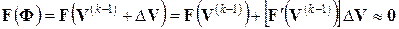. (65)

Здесь 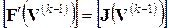– матрица Якоби для системы уравнений

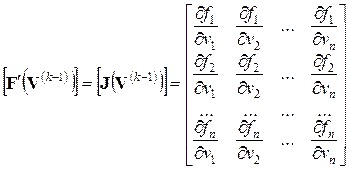
Полагая, что матрица Якоби 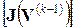неособенная, т.е. существует обратная матрица, разрешим уравнение (65) относительно вектора :

.

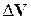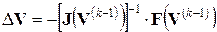Здесь 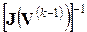– обратная матрица матрицы Якоби.

Подставив значение приращения 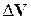в уравнение (64), получаем алгоритм метода Ньютона

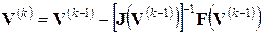(66)

Здесь вместо точного решения 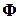системы (60) в левой части алгоритма (66) поставлено последующее приближение 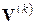к решению, так как значение приращения 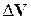получено из приближенного уравнения (65). При расчете по формуле (66) на каждом шаге итерации необходимо вычислять обратную матрицу 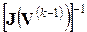при новых значениях 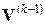. Расчеты продолжаются до выполнения условия сходимости решения, т.е. близости двух последовательных приближений

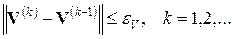(67)

где e_V – малая величина, погрешность решения.

Этот метод обладает значительно большей скоростью сходимости, чем метод простой итерации. Для его применения необходимо, чтобы матрица Якоби была неособенной, т.е. имела обратную матрицу.

Т.о. метод Ньютона использует информацию о производных функций для определения направления движения на итерации вдоль линий касательных, построенных из начальной точки итерации, причем в качестве конечной принимается точка с координатами пересечения касательных с осями переменных.

Проиллюстрируем метод Ньютона на примере функции одной переменной 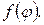Пусть уравнение имеет вид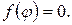

Уравнение касательной к функции 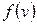в точке :

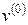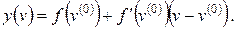
В конечной точке итераци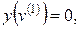и или

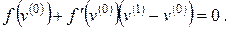
Тогда

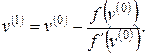
В заключение следует отметить, что скорость сходимости итерационных методов во многом зависит от близости выбора начальных данных к решению задачи. При неудачном выборе начальных данных итерационный процесс может не сойтись.