Метод Гаусса-Зейделя

Это один из итерационных методов решения систем линейных алгебраических уравнений, поэтому требуется задать начальную точку итерационного процесса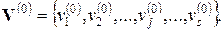

Система уравнений на k-ой итерации преобразована в форму явных зависимостей, позволяющих последовательно определять все переменные следующей итерационной точки.

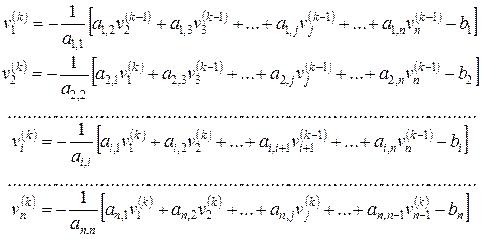(59)

Сходимость метода на текущей операции оценивается уменьшением длины вектора невязок системы уравнений: 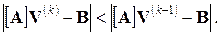Решение системы уравнений считается найденным, если выполняется условие требуемой точности вычислений: 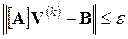. Иногда принимают упрощенное условие окончания итерационного процесса 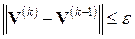, где 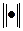обозначена норма вектора, характеризующая его длину. Существует три общепринятых нормы векторов:

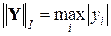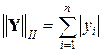1. ; 2. ; 3. 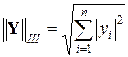. Какую из этих норм принять – вопрос не принципиальный.

Несколько замечаний.

1. Метод особенно эффективен на задачах большой размерности с разреженными матрицами [A], требует меньшего объема оперативной памяти и машинного времени.

2. Метод применим не для любой системы линейных уравнений, т.к. решение может не сходиться, т.е. последующая итерация дает большую невязку, чем предыдущая. Условие сходимости итерационного процесса – все корни l_i уравнения 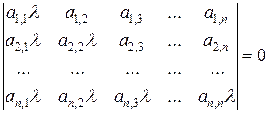по модулю должны быть меньше 1. Найти эти корни порой непросто, поэтому другой достаточный вариант условия сходимости итерационного процесса – это диагональное доминирование: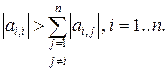

3. Учитывая замечание 2, требуется подготовка системы линейных уравнений к расчету, которая состоит в перестановке уравнений таким образом, чтобы наибольшие по модулю коэффициенты стояли на диагонали матрицы.