Метод Гаусса

Уравнения независимые и совместные, т.е. не противоречат друг другу.

Метод Гаусса – это наиболее распространенный из всех существующих прямых численных методов решения систем линейных алгебраических уравнений с плотно заполненной матрицей коэффициентов [A]. Метод успешно работает на задачах любой размерности.

Алгоритм метода включает два хода:

· прямой ход – последовательное исключение переменных из уравнений за счет приведения матрицы [A] к виду верхней треугольной;

· обратный ход – последовательное определение переменных из явно выраженных уравнений преобразованной системы.

Прямой ход предполагает выполнение n-1 этапов исключения переменных из уравнений и обнуления левой нижней части матрицы [A]. Для пересчета коэффициентов уравнений преобразуемой строки используются соотношения:

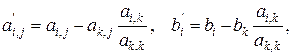(50)

где без штрихов указаны текущие значения коэффициентов и свободных членов уравнений, а со штрихами – вычисляемые значения. Вычисления производятся циклически, где внешний цикл по переменной k = 1..n-1, средний цикл по переменной i = k+1..n, а внутренний цикл по переменной j = k..n.

Обратный ход:

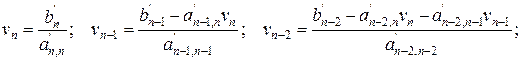и т. д. (51)

Для успешной реализации метода необходимо выполнить два условия:

1. Все коэффициенты, стоящие по главной диагонали матрицы [A] должны быть отличны от 0;

2. Они должны быть по модулю как можно больше.

Первое условие понятно: при пересчете коэффициентов матрицы [A]и вектора B на них приходится делить. Второе условие не столь очевидно. Если коэффициент близок к нулю, то при делении на него получатся очень большие по модулю новые коэффициенты. При обратном ходе неточные значения неизвестных v_i будут умножаться на них, что приведет к резкой потере точности решения. Погрешности найденных решений связаны с многократным пересчетом коэффициентов матрицы [A]и вектора B, причем каждый пересчет сопровождается округлением найденного значения.

Для выполнения указанных условий приходится уравнения менять местами, при этом меняются местами строки как матрицы А, так и вектора В.