МЕТОДЫ РАСЧЕТА И АНАЛИЗА ПАРАМЕТРОВ

МАТЕМАТИЧЕСКИХ МОДЕЛЕЙ

Основные понятия и определения методов анализа

Мы уделили довольно много времени на составление математических моделей различных систем. Но вспомним, с какой целью мы это делали. Это мы делали с целью замены реального процесса, изучение которого связано с технической сложностью, дороговизной или просто невозможно.

Совершенно очевидно, что математические модели в форме систем различных видов уравнений, не являются полноценными с точки зрения их способности ответить на вопросы типа:

· Как влияют на параметры процесса исходные данные?

· Как влияют внешние воздействия на данный процесс? и т.п.

Очевидно, что необходимо изменение формы представления модели таким образом, чтобы можно было использовать ее при действиях с численными данными. Такая форма представления называется алгоритмом математической модели, а последовательность выполнения отдельных этапов алгоритма определяется методами расчета и анализа переменных и параметров модели.

Методы расчета и анализа разделяют на две группы:

1. Аналитические методы, дающие точные решения уравнений ММ в виде явных зависимостей физических переменных от пространственно-временных параметров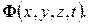

2. Численные (алгоритмические) методы, обеспечивающие получение некоторых приближенных решений на основе реализации прямых или итерационных численных алгоритмов, как заданной последовательности действий с числами. Приближенные значения физических переменных 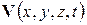характеризуются погрешностями

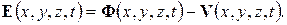
Прямые численные методыосновываются на последовательном преобразовании системы связанных уравнений ММ с целью получения отдельных уравнений аналитического вида за счет выполнения определенного числа операций пересчета исходных данных или внутренних параметров. При этом многократное изменение исходных данных приводит к накоплению погрешностей, что отражается на результирующей погрешности в расчетных приближенных значениях переменных.

Итерационные численные методы строятся на выполнении некоторого числа последовательных приближений решения уравнений модели к точному при неизменных исходных данных. Как правило, общее количество итераций, необходимых для анализа модели, заранее не известно и зависит как от самого алгоритма численного метода, так и от вида и размерности систем уравнений.

В итерационных методах отсутствуют накопления погрешностей исходных данных и при выполнении условий их сходимости точность этих методов выше, чем прямых. При использовании итерационных методов необходимо либо знать, либо назначить некоторое исходное (начальное) решение 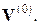Далее выполняется последовательность итераций:

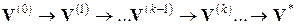
В теории приближенных вычислений используются несколько принципиальных понятий, которые характеризуют численные методы:

· Устойчивость– свойство численного метода, характеризующее степень чувствительности погрешности приближенных решений модели к погрешностям в исходных данных. Иными словами, метод обладает достаточной устойчивостью, если малые изменения (погрешности) в исходных данных приводят к соизмеримым по величине погрешностям приближенных значений физических переменных.

· Сходимостьчисленного метода отражает близость приближенного решения к точному и не связывается с факторами накопления погрешностей. Для итерационных методов основным условием сходимости является регулярное снижение погрешности приближенного решения при бесконечном увеличении числа итераций, т.е.

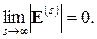
Для прямых методов решения дифференциальных уравнений с аппроксимацией производных на разностной сетке сходимость обуславливается размерами сетки, а именно: при бесконечном измельчении размеров сетки 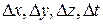приближенная (сеточная) функция аппроксимирует точную и погрешность стремится к нулю

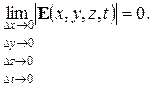
· Матрица Якоби (якобиан – определитель матрицы Якоби)– показывает чувствительность уравнений модели к изменению физических переменных. Так для систем ОДУ или АУ:

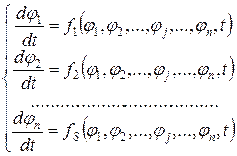
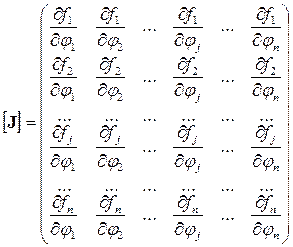(48)

Матрица Якоби достаточно широко используется как при предварительной оценке устойчивости численных методов, так и непосредственно в алгоритмах самих методов в качестве инструмента при выборе направления итерационного процесса. При этом метод будет устойчив, если влияние различных переменных модели на решение системы уравнений будет относительно соизмеримо. Иными словами, если модель одновременно описывает процессы, в которых пространственно-временные градиенты переменных имеют существенные различия, это неизбежно скажется на снижении устойчивости численного метода. Исследуя матрицу Якоби на спектр собственных чисел и определяя степень их различия, проводится анализ характера обусловленности (чувствительности) системы уравнений к изменению переменных и оценка возможности использования численного метода по устойчивости.

В последующих разделах, не вдаваясь в теоретические вопросы исследования численных методов, будут представлены наиболее известные и часто используемые алгоритмы, позволяющие самостоятельно провести программную разработку задачи или сделать грамотный выбор уже существующих программных средств.