Решение систем линейных алгебраических уравнений. С системами линейных алгебраических уравнений вы знакомы еще со школьной поры и знаете, как их можно решить

С системами линейных алгебраических уравнений вы знакомы еще со школьной поры и знаете, как их можно решить. Первый метод их решения – это метод подстановки, второй – по правилу Крамера. Это достаточно простые методы. Но имеют один очень существенный недостаток – они не годятся для решения систем с большим количеством уравнений, решения получаются чрезвычайно громоздкими. В инженерной практике приходится решать системы линейных уравнений, включающие десятки, сотни, а иногда и тысячи уравнений. По этой причине разработан ряд методов, имеющих значительно меньшую трудоемкость и лучше приспособленных для программной реализации.

Пусть система линейных алгебраических уравнений имеет вид:

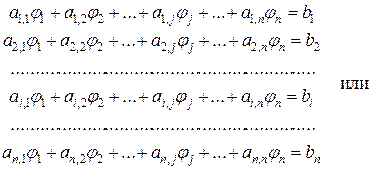[A]Ф - B = 0.(49)

[A]V - B = - [A]E.

Очевидно, что сложность системы линейных уравнений определяется структурой ее матрицы А. Существуют два случая, когда система имеет простые решения. Если А – диагональная матрица

,

то система распадается на n независимых уравнений, каждое их которых содержит одну неизвестную величину, и проблем с вычислениями не возникает.

Просто решается задача и в случае, когда матрица А является треугольной

.

В этом случае из последнего уравнения следует 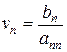, и далее

для

Большинство прямых методов решения системы линейных уравнений, используемых на практике, основаны на приведении исходной матрицы к треугольному виду с последующим нахождением неизвестных по рассмотренным выше формулам. Одним из таких методов является метод исключения Гаусса.