Метод прогонки

Метод используется для решения систем линейных уравнений с трехдиагональной матрицей коэффициентов. Система уравнений имеет вид:

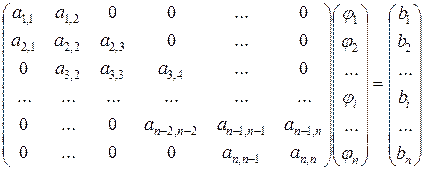. (54)

Метод базируется на линейных зависимостях между значениями переменных: 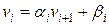, (55)

где 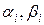– прогоночные коэффициенты, соответствующие i-ому уравнению.

Метод включает также два хода:

· прямой ход – вычисление прогоночных коэффициентов для всех i = 1..n-1;

· обратный ход – последовательный расчет всех переменных, начиная с последнего уравнения.

В соответствии с выражением (54) первое уравнение записывается:

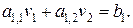
Отсюда 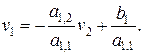Т.о., прогоночные коэффициенты для первого уравнения: 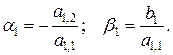(56)

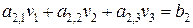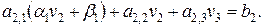Запишем второе уравнение системы: или Тогда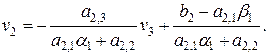

Т.о., для всех уравнений системы, начиная со второго, прогоночные коэффициенты рассчитываются по зависимостям:

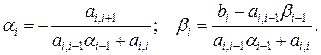(57)

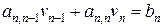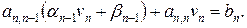Обратный ход. Запишем последнее уравнение системы: или Тогда

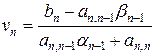. (58)

Далее определяются все остальные переменные, используя принятые линейные зависимости (55).