Метод LU-разложения матрицы коэффициентов

Метод основан на представлении матрицы системы в виде произведения двух матриц 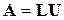, где L– нижнетреугольная матрица с единичной диагональю, а U– верхнетреугольная матрица.

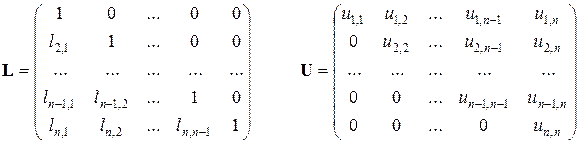
Запишем систему 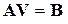в виде .

Обозначим 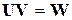, (52)

тогда . (53)

Порядок заполнения матриц Lи U:

1. Заполняем диагональ матрицы Lединицами;

2. Заполняем элементы обеих матриц, равные 0;

3. Заполняем первую строку матрицы Uсоответствующими элементами матрицы А;

4. Заполняем первый столбец матрицы Lэлементами, равными 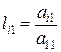, i = 2..n;

5. Поочередно заполняем строки матрицы U и столбцы матрицы L, пользуясь формулами

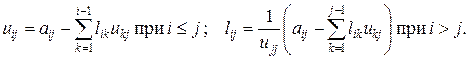
Решаем сначала систему (53), находим последовательно w₁, w₂, …, w_n, а потом систему (52), находим последовательно v_n, v_n-1, …, v₁.

Для повышения точности вычислений также требуется перестановка уравнений таким образом, чтобы по диагонали стояли наибольшие коэффициенты.

Метод особенно удобен при решении множества систем уравнений, у которых отличаются только правые части. В этом случае разложение матрицы выполняется только один раз, а решение уравнений сводится только к решению систем (52) и (53).