Метод Рунге-Кутты
Методы Рунге-Кутты (распространено неправильное название «методы Рунге-Кутта») – важное семейство численных алгоритмов решения обыкновенных дифференциальных уравнений и их систем. Данные итеративные методы явного и неявного приближённого вычисления были разработаны около 1900 года немецкими математиками Карлом Рунге и Мартином Вильгельмом Куттой.
Формально, методом Рунге-Кутты является модифицированный и исправленный метод Эйлера, они представляют собой схемы второго порядка точности. Существуют стандартные схемы третьего порядка, не получившие широкого распространения. Наиболее часто используется и реализована в различных математических пакетах стандартная схема четвёртого порядка.
Метод Рунге-Кутты 4 порядка столь широко распространён, что его часто называют просто методом Рунге-Кутты.
Рассмотрим задачу Коши 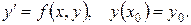
Тогда приближенное значение в последующих точках вычисляется по итерационной формуле:
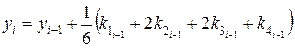 (79)
(79)
Вычисление нового значения проходит в четыре стадии:
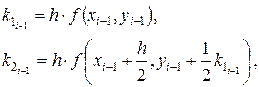
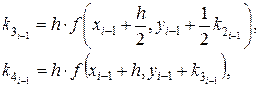
где h – величина шага сетки по x.
Этот метод имеет четвёртый порядок точности, то есть суммарная ошибка на конечном интервале интегрирования имеет порядок 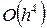 (ошибка на каждом шаге порядка
(ошибка на каждом шаге порядка 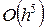 ).
).
Для системы обыкновенных дифференциальных уравнений 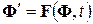 все вычисляется аналогично:
все вычисляется аналогично:
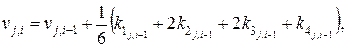 где (80)
где (80)
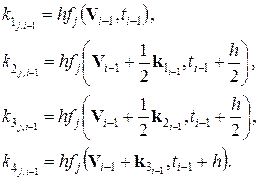
Дата добавления: 2015-06-10; просмотров: 750;
