Одномерная динамическая модель

Рассмотрим пространственно-временную сетку и шаблоны «правый нижний уголок» и «правый верхний уголок», используемые для численного исследования процесса течения газа в одномерном газопроводе с узлами «i,k». Принцип аппроксимации производных покажем на примере уравнения сохранения вещества, считая, что в пределах размеров одной ячейки сетки скорость течения газа положительна и постоянна V_x > 0.

Для шаблона «правый нижний уголок»:

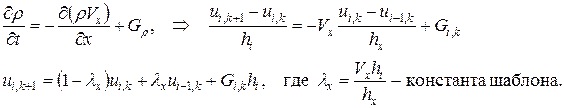(84)

Константа шаблона характеризует соотношение между размерами ячейки и скоростями распространения волн возмущения в газовом потоке. При этом устойчивость метода зависит от размеров ячейки и оценивается критерием Куранта, согласно которому перемещение фронта волны возмущения, имеющего скорость 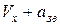, за интервал времени h_t не должно превышать величины размера ячейки h_x, т. е. 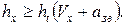Таким образом, константа шаблона, обеспечивающая достаточную устойчивость численного метода, определяется из условия Куранта с учетом введения коэффициента запаса по устойчивости: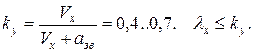

Для шаблона «правый верхний уголок»:

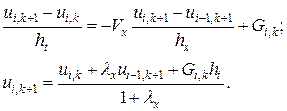(85)

Начальные условия задаются в узлах сетки: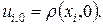

Граничные условия: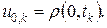

Соответствующие шаблоны для аппроксимации уравнений двумерной динамической модели:

Для первого из этих шаблонов:

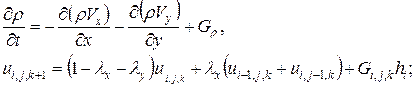(86)

для второго

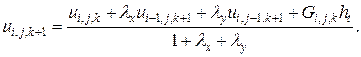(87)

Начальные условия: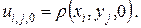

Граничные условия: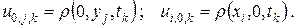

Для трехмерной динамической модели шаблонов по понятным соображениям не существует, но разностные уравнения записать можно, опираясь на выражения (84) - (87).