Распределенных одномерных статических моделей

Данные модели включают системы дифференциальных уравнений второго порядка с граничными условиями на левом и правом краях одномерной физической области, что обуславливает их название, как «краевые» задачи:

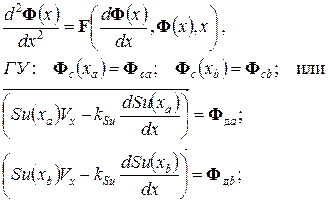(81)

Рассмотрим методы решения подобных моделей.

Метод пристрелки является универсальным как для численного решения линейных, так и нелинейных уравнений и носит итерационный характер. Алгоритм этого метода основан на замене дифференциальных уравнений второго порядка двумя уравнениями первого порядка и выполнении ряда последовательных решений задач Коши с варьируемыми начальными условиями.

Уравнение второго порядка с граничными условиями слева и справа

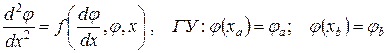
представим в виде двух уравнений:

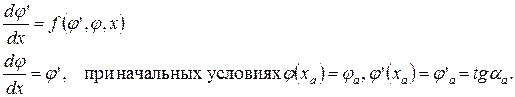
Каждое решение задачи Коши при заданном начальном условии по углу наклона касательной в начальном левом узле сетки дает значение сеточной функции в крайнем правом узле и оценка сходимости метода проводится по наличию отклонения этого значения от точного граничного условия на правой границе. После выполнения определенного числа итераций (решений задачи Коши на сетке) полученная сеточная функция в достаточной степени приближается к точному решению, что оценивается условием: .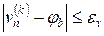

Проиллюстрируем алгоритм метода пристрелки.

Метод конечных разностей используется для численного решения линейных дифференциальных уравнений и основан на принципе аппроксимации производных.

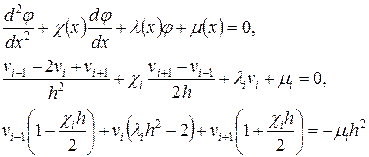(82)

Уравнения вида (82), записанные для всех внутренних узлов сетки i = 1..n образуют систему линейных уравнений с трехдиагональной матрицей.

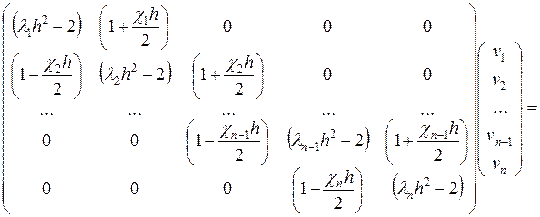
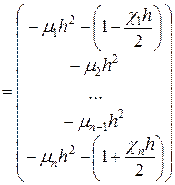(83)

Для решения системы (83) используется метод прогонки.