Аналитические решения распределенных статических одномерных моделей для некоторых характерных тепловых процессов в технических объектах
1. Моделирование статического процесса теплопередачи через плоскую твердую стенку между двумя жидкими средами.
Известно: h – толщина стенки; λ – коэффициент теплопроводности материала стенки; Tca, aa – температура среды и коэффициент теплоотдачи между средой и стенкой слева от нее; Tcb, ab – температура среды и коэффициент теплоотдачи между средой и стенкой справа от нее.
Требуется получить зависимость температуры по толщине стенки.
Модель одномерная статическая. Вещество внутри стенки не перемещается, поэтому в уравнении (16) будет присутствовать только микропоток тепловой энергии.
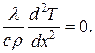 Отсюда
Отсюда 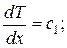
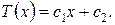
ГУ слева: 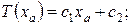
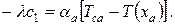
ГУ справа: 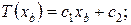
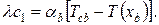
Температурное поле в стенке T(x) линейно относительно координаты x. Граничные условия образуют систему из четырех алгебраических линейных уравнений относительно неизвестных 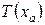 ,
, 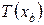 , c1, c2.
, c1, c2.
2. Моделирование статического процесса теплообмена между потоком нагретой жидкости, движущегося в прямолинейном трубопроводе с постоянной площадью сечения через его боковую цилиндрическую стенку.
Известно: d – средний диаметр трубопровода; L – длина трубопровода; rж, сж – плотность и теплоемкость жидкости-теплоносителя; Vж – средняя скорость движения жидкости в трубопроводе; Ta – температура втекающего в трубопровод потока жидкости (граничное условие); Tcб, aб – температура стенки и коэффициент теплоотдачи между жидкостью и боковой поверхностью трубопровода.
Требуется получить зависимость изменения температуры теплоносителя по длине трубопровода.
Задача моделирования решается без учета микропотока тепловой энергии, а отвод ее через боковую стенку определяется через использование условной скорости исчезновения субстанции внутри самой системы, что возможно для осесимметричных объектов.
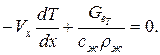 Используя уравнение (10), получим:
Используя уравнение (10), получим: 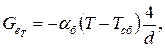
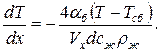
ГУ: при x = 0 T(0) = Ta.
Решение уравнения:
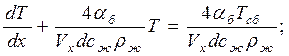
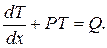
Найдем общее решение однородного уравнения 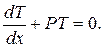
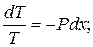
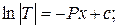
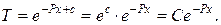
Заменим постоянную С неизвестной функцией u(x), тогда 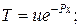 а
а 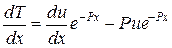 . Подставим эти значения в неоднородное уравнение
. Подставим эти значения в неоднородное уравнение 
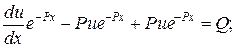
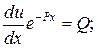
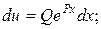
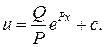
Тогда 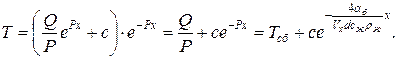
Константу интегрирования найдем из граничного условия
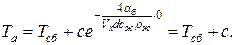 Отсюда
Отсюда 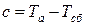 .
.
Тогда
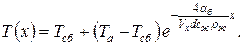
3. Моделирование сосредоточенного динамического процесса нагрева (охлаждения) геометрического объекта с осредненной температурой при наличии нескольких тепловых потоков, действующих через отдельные граничные поверхности.
Известно: W – объем объекта; r, ст – плотность и теплоемкость материала объекта; SГi и aбi – площадь граничной поверхности и соответствующий коэффициент теплоотдачи между i-ой боковой поверхностью и средой (i = 1.. n); T0 – начальная температура объекта; Tсб – температура внешней среды.
Требуется найти зависимость температуры объекта от времени.
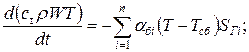
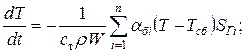
НУ: 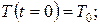
Решение уравнения:
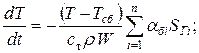
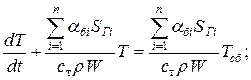
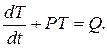
Получилось уравнение, аналогичное тому, что решали в предыдущем примере. 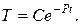 Заменим константу С на неизвестную функцию u(t).
Заменим константу С на неизвестную функцию u(t).
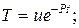
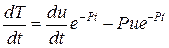 . Подставим эти значения в неоднородное уравнение
. Подставим эти значения в неоднородное уравнение 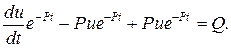
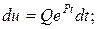
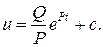
Тогда 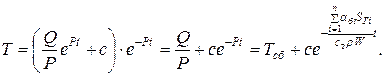
Константу интегрирования найдем из начального условия
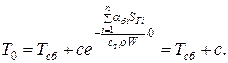 Отсюда
Отсюда 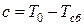 .
.
Тогда
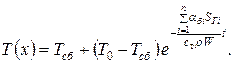
Математические модели газодинамических систем (ММ ГДС)
В газодинамических системах происходят процессы сжатия, расширения и движения потоков газовой среды при действии на нее внешних возмущающих факторов в виде дополнительного подвода или отвода газа. При формировании ММ для газообразных сжимаемых сред можно принять допущения:
1. Гравитационной составляющей энергии в виду ее относительной малости в сравнении с другими формами энергии можно пренебречь;
2. Влияние относительно низкой вязкости газа на изменение количества движения потока незначительно и может не учитываться.
Распределенные модели (динамическая, трехмерная)
В качестве субстанций принимаются все возможные виды:
· вещество (плотность газа): r ;
· количество движения: 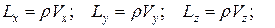
· энергия: 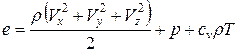 .
.
Для сжимаемой среды можно объединить деформационную и тепловую составляющие энергии. Учитывая то, что 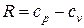 ,
, 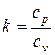 и
и 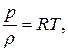 получим:
получим:
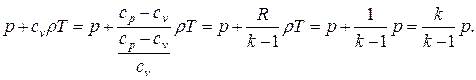
Макропотоки субстанций:
· вещества: 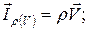
· количества движения: 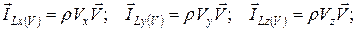
· энергии: 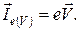
Микропотоки субстанций для ГДС связаны с диффузионными процессами и вязкостью среды и в большинстве задач не рассматриваются.
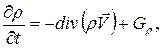 – уравнение сохранения вещества (19)
– уравнение сохранения вещества (19)
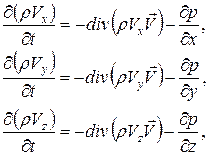 – уравнения сохранения количества движения (20)
– уравнения сохранения количества движения (20)
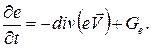 – уравнение сохранения энергии (21)
– уравнение сохранения энергии (21)
В уравнениях (20) изменение количества движения происходит и за счет наличия градиентов давлений между соседними слоями движущегося потока, что отражено через параметры:
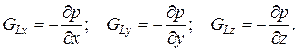
Начальные и граничные условия:
НУ: 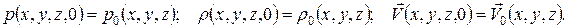
ГУ: для 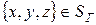
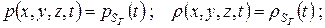
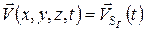
или 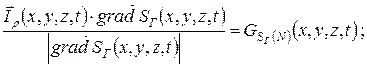
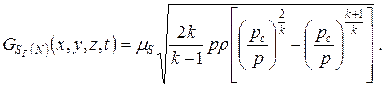
Последнее выражение определяет удельный массовый расход газа для подкритического режима течения через отверстие площадью Sг как открытую для вещества граничную поверхность, т.е. при 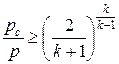 .
.
Здесь pc – значение противодавления в газовой среде, куда истекает рассматриваемый поток, 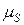 – коэффициент расхода.
– коэффициент расхода.
Если 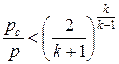 , то истечение происходит с критической скоростью и удельный массовый расход равен
, то истечение происходит с критической скоростью и удельный массовый расход равен
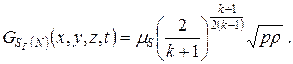
Распределенные одномерные модели (динамические или статические)
Одномерная модель характеризует процессы течения газового потока в газопроводе и представляет собой систему из трех уравнений в частных производных:
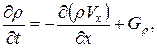
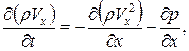 (22)
(22) 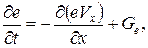
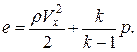
НУ: 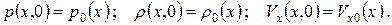
ГУ: для x = xa 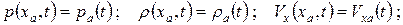
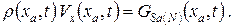
Дата добавления: 2015-06-10; просмотров: 1952;
