Сосредоточенные динамические модели. Сосредоточенную газодинамическую область, в которой за счет наличия втекающих и вытекающих потоков происходит изменение давления и плотности
Сосредоточенную газодинамическую область, в которой за счет наличия втекающих и вытекающих потоков происходит изменение давления и плотности, можно представить следующим образом:
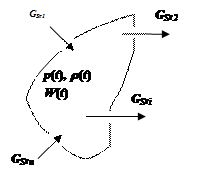 Уравнение сохранения вещества:
Уравнение сохранения вещества:
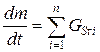 ,
, 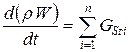 ,
,
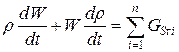 ,
,
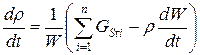 (23)
(23)
Сначала рассмотрим случай, когда есть один втекающий поток газа, т. е. две подсистемы – ведущая (0) и подчиненная (1). Уравнение сохранения энергии запишем в виде первого начала термодинамики
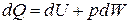 .
.
Изменение количества теплоты в системе равно алгебраической сумме изменений за счет потока втекающего газа и за счет потерь теплоты вследствие теплообмена с соседними системами
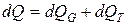 .
.
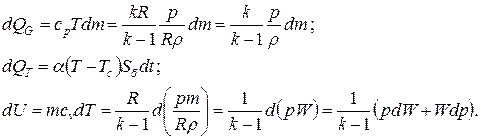
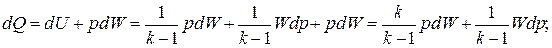
С другой стороны
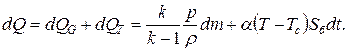
Приравняем эти выражения, выделим dp и разделим на dt.
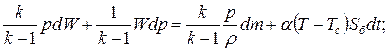
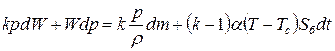 ;
;
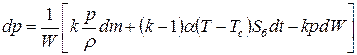 ;
;
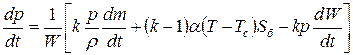 ;
;
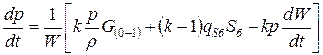 . (24)
. (24)
Расход через отверстие вычисляется по формулам:
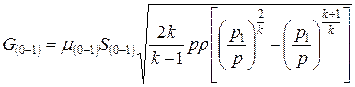 для подкритического режима, т.е. при выполнении условия
для подкритического режима, т.е. при выполнении условия 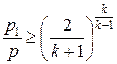 . В противном случае при критическом режиме течения
. В противном случае при критическом режиме течения
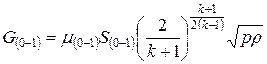 .
.
Для нескольких взаимодействующих газодинамических систем с учетом направления движения газовых потоков уравнение сохранения энергии (24) запишется в виде:
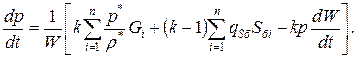 (25)
(25)
Здесь 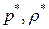 – определяющие давление и плотность газа.
– определяющие давление и плотность газа.
Если поток вытекающий Gi< 0, в качестве определяющих принимаются параметры в рассматриваемой системе, т.е. 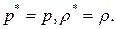
Если поток втекающий Gi> 0, в качестве определяющих принимаются параметры в соседней системе, т.е. 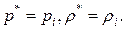
Скорость изменения объема ГДС зависит от конструктивной схемы:
· для жестких резервуаров 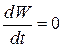 ;
;
· для цилиндрических объемов с подвижным дном величина 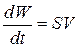 определяется поперечной площадью цилиндра S и скоростью подвижного дна V;
определяется поперечной площадью цилиндра S и скоростью подвижного дна V;
· для упругих резервуаров изменение объема зависит от изменения давления через коэффициент податливости kL в а) линейной или б) нелинейной формах.
а) 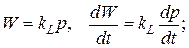 б)
б) 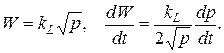
Математические модели гидромеханических систем (ММ ГМС)
В гидромеханических системах происходят процессы вытеснения и движения потоков несжимаемой и вязкой среды, обладающей достаточно высокой плотностью. Процессы в ГМС связаны с воздействием на них внешних гидравлических потоков, подводящих или отводящих жидкость из системы.
При формировании ММ ГМС в качестве основы используем рассмотренные выше модели для газодинамических систем с условиями постоянства плотности среды, наличия микропотоков количества движения, связанных с вязкостью, а также внутренним изменением количества движения от гравитационных сил.
Распределенные модели (динамическая, трехмерная)
В качестве субстанций принимаются все возможные виды:
· вещество (плотность жидкости) r ;
· количество движения: 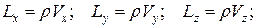
· энергия: 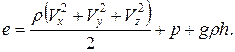
Макропотоки субстанций:
· вещества: 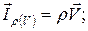
· количества движения: 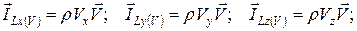
· энергии: 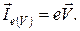
Вязкость жидкости учитывается в уравнениях сохранения количества движения в качестве микропотоков, а именно:
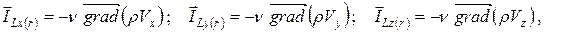
где n – коэффициент кинематической вязкости жидкости.
Уравнение сохранения вещества:
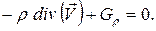 Для
Для 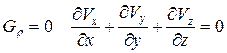 (26)
(26)
Уравнение сохранения количества движения вдоль оси x:
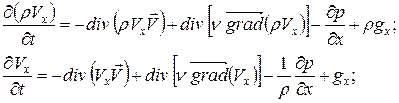
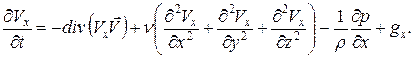 (27)
(27)
Используя выражение (27), запишем уравнения сохранения количества движения по двум остальным осям:
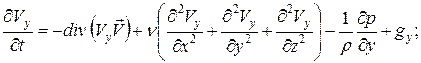 (28)
(28)
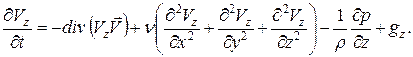 (29)
(29)
Закон сохранения количества движения для ГМС можно выразить также через полные производные субстанции по времени. Покажем это преобразование на примере выражения (27).
Полная производная имеет вид: 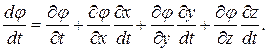
Тогда выражение (27) можно записать как
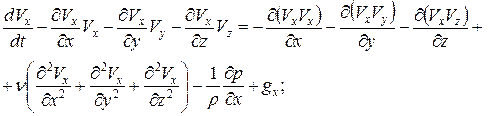
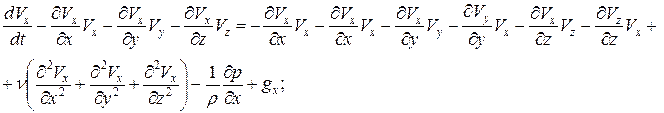
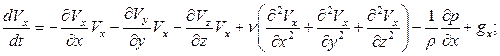
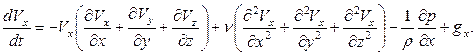
Учитывая выражение (26), получим
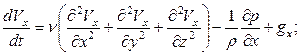
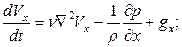 (30)
(30)
Аналогично 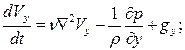 (31)
(31)
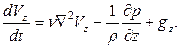 (32)
(32)
Покажем, что закон сохранения энергии для гидромеханических систем вырождается и может быть использован при моделировании только лишь в части сохранения тепловой энергии.
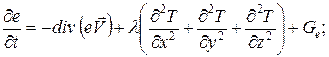
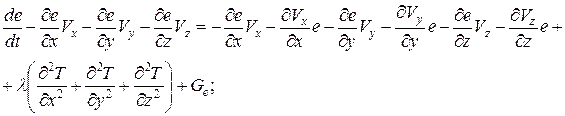
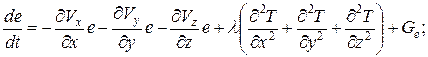
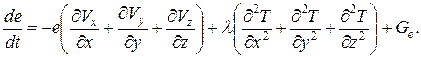
Учитывая выражение (26), получим
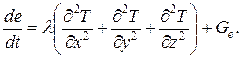
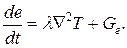
Отсюда следует, что изменение по времени энергии в гидромеханической системе за счет действия макропотоков отсутствует, т.е. запас энергии в системе постоянен (при отсутствии теплообмена).
Начальные и граничные условия:
НУ: 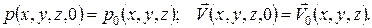
ГУ: для 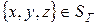
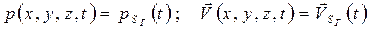
или 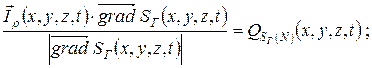
Распределенные одномерные модели (динамические и статические)
Одномерная модель характеризует процессы течения жидкости в гидропроводе. Для гидропровода с постоянной площадью поперечного сечения:
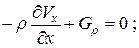 Для
Для 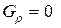
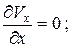 (33)
(33)
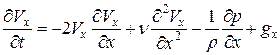 или
или 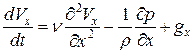 (34)
(34)
НУ: 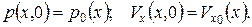
ГУ: для 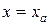
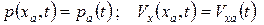 ;
;
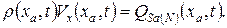
Для гидропривода с переменной площадью поперечного сечения уравнение сохранения вещества (неразрывности потока) можно видоизменить, если в качестве субстанции рассматривать массу жидкости, отнесенную к единице длины гидропровода, т.е.
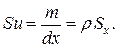
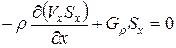 . (35)
. (35)
Дата добавления: 2015-06-10; просмотров: 916;
