Статических одномерных моделей
Закон сохранения субстанций для статических одномерных моделей имеет вид:
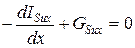 или
или 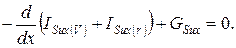
С учетом выражений для потоков субстанций (5) и (6)
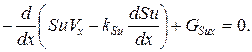
Если принять линейную зависимость параметра скорости внутренней генерации от величины запаса субстанции в системе, то закон сохранения примет вид линейного неоднородного дифференциального уравнения второго порядка с постоянными коэффициентами:
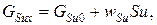
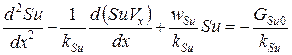 . (11)
. (11)
Если скорость движения среды Vx =const,получим
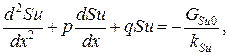 где
где 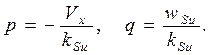
Напомню, что общее решение неоднородного дифференциального уравнения с постоянными коэффициентами можно получить, суммируя общее решение соответствующего однородного уравнения (yo) с частным решением неоднородного уравнения (y*). Для нахождения общего решения однородного уравнения надо решить алгебраическое (характеристическое) уравнение. В нашем случае это квадратное уравнение 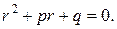 В зависимости от вида корней характеристического уравнения общее решение однородного уравнения примет вид:
В зависимости от вида корней характеристического уравнения общее решение однородного уравнения примет вид:
Если корни действительныеи r1¹ r2, 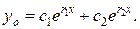
Если корни действительные и r1=r2= 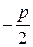 ,
, 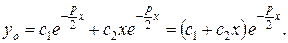
Если корни комплексные сопряженные 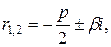 где
где 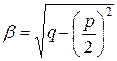 ,
,
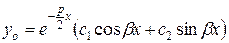 .
.
Найдем частные решения неоднородного уравнения.
Если правая часть 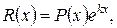 где
где 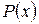 – многочлен степени m, а k не является корнем характеристического уравнения, то
– многочлен степени m, а k не является корнем характеристического уравнения, то 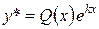 , где
, где 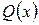 – некоторый многочлен той же степени m.
– некоторый многочлен той же степени m.
Если правая часть 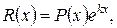 где
где 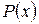 – многочлен степени m, а k является одним из неравных корней характеристического уравнения, то
– многочлен степени m, а k является одним из неравных корней характеристического уравнения, то 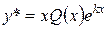 , где
, где 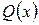 – некоторый многочлен той же степени m.
– некоторый многочлен той же степени m.
Если правая часть 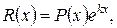 где
где 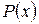 – многочлен степени m, а k дважды является корнем характеристического уравнения, то
– многочлен степени m, а k дважды является корнем характеристического уравнения, то 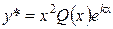 , где
, где 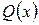 – некоторый многочлен той же степени m.
– некоторый многочлен той же степени m.
В нашем случае правая часть уравнения представляет собой константу, т.е. многочлен нулевой степени, а k = 0. Т.к. p ¹ 0 и q ¹ 0, то корень характеристического уравнения не может быть равен 0. Тогда частное решение неоднородного уравнения y* будет представлять собой константу: 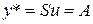 . Подставим это решение в уравнение и вычислим A.
. Подставим это решение в уравнение и вычислим A.
При Su=const 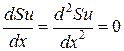 . Тогда уравнение примет вид
. Тогда уравнение примет вид
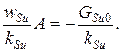 Частное решение неоднородного уравнения
Частное решение неоднородного уравнения
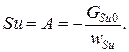
Общее решение неоднородного уравнения:
· при действительных и неравных r1 и r2
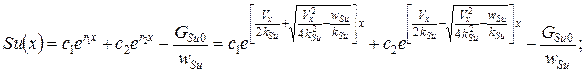 (12)
(12)
· при действительных и равных r1 и r2
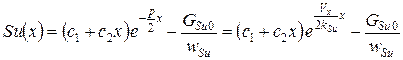 ; (13)
; (13)
· при комплексных сопряженных корнях
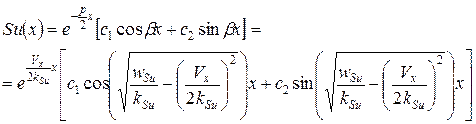 . (14)
. (14)
Граничные условия задаем по левой x = xa и правой x = xb границам одномерной распределенной области системы. При этом для определенности будем считать направление вектора-градиента поверхности границы в сторону от рассматриваемой системы, т.е. на границе Sга этот вектор отрицательный и направлен влево, а на границе Sгb – положительный и направлен вправо:
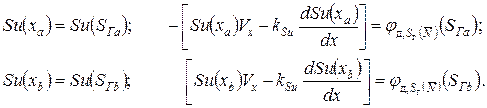
Постоянные c1 и c2 определяются из граничных условий. Например, для случая действительных и разных корней r1 и r2 необходимо решить систему уравнений:
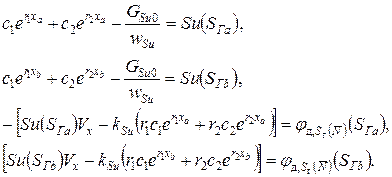
Дата добавления: 2015-06-10; просмотров: 1032;
