Для сокращения размерности модели

Мы живем в трехмерном мире, поэтому математические модели реальных процессов тоже должны быть трехмерными в пространстве. Однако, чем больше размерность математической модели, тем она становится сложнее. На этапе составления ММ это усложнение выражается в ее громоздкости, но на этапе ее решения трудности возрастают явно нелинейно по отношению к размерности модели. Поэтому, с целью упрощения решения задач анализа моделей, при сохранении приемлемой достоверности и точности результатов целесообразно уменьшить пространственную размерность моделей за счет использования свойств геометрической симметрии области системы.

Например, если область системы представляет собой канал круглого поперечного сечения, симметричный относительно оси z, то целесообразно рассматривать задачу не в прямоугольной {x, y, z}, а в цилиндрической системе координат {r, j, z}. В этом случае можно предполагать, что угловая координата j не будет влиять на параметры процесса, и можно перейти от объемной к плоской задаче. Если можно пренебречь изменением параметров системы по радиальной координате, то от двухмерной модели в координатах { r, z } можно перейти к одномерной, зависящей только от z. При постоянной площади поперечного сечения области системы такой переход выглядит вполне обоснованным. Но подобное упрощение ММ возможно и при области системы с переменной площадью поперечного сечения за счет учета составляющей потока субстанции в радиальном направлении через параметр, характеризующий скорость внутренней генерации или уничтожения субстанции в дивергентной форме закона сохранения (7).

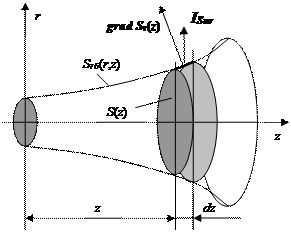На рисунке показана осесимметричная область, ограниченная боковой поверхностью S_rб (r, z). Выделенный объем dW толщиной dz считаем сосредоточенной элементарной подсистемой с осредненными физическими переменными.

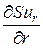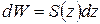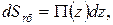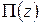Интенсивность изменения потока субстанции в направлении оси r можно условно представить через скорость изменения субстанции в объеме среды через элементарную боковую поверхность где – периметр симметричной области, изменяющийся по длине.

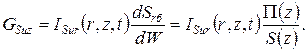(10)