Понятие субстанций, их формы и потоки
Прежде всего, остановимся на термине «субстанция». Это философский термин, который означает сущность; то, что лежит в основе; то, что существует самостоятельно, само по себе. Традиционно философы выделяют два вида субстанции – Дух и Материю в соответствии с двумя ответами на основной вопрос философии. Зачем мы будем использовать этот термин? Просто надо как-то называть одним словом ряд физических понятий, для которых подобрать точный термин не удалось. Поэтому будем использовать этот термин, мысленно заключив его в кавычки.
Под субстанцией будем понимать фундаментальную физическую категорию, объединяющую переменные состояния отдельной физической системы и сохраняющую свой полный запас для совокупности взаимодействующих систем, образующих функционирующий технический объект. Субстанция, как и физические переменные, зависит от пространства и времени: Su(x, y, z, t).
Субстанция – это общее название таких величин, как:
· масса (вещество) Su(x, y, z, t) = r (x, y, z, t) [кг/м3];
· количество движения (вектор)
Su(x, y, z, t) = {Sux; Suy; Suz} = {rVx; rVy; rVz} [кг/с∙м2];
· энергия
Su(x, y, z, t) = e(x, y, z, t) =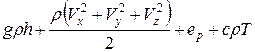 
[Дж/м3].
Представленные формы субстанций отнесены к единице объема физической среды. Полная удельная энергия показана как сумма гравитационной, кинетической, деформационной и тепловой составляющих.
Как вы, наверное, уже заметили, для субстанций существуют известные законы сохранения.
Передача субстанций в среде физических систем и по границам между системами обусловлена наличием так называемых потоков субстанций.
Макропоток обеспечивает передачу субстанции вместе с частицами подвижной жидкой или газообразной среды, а также с механическими макросистемами. Макропоток определяется запасом субстанции и скоростью движения среды:
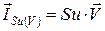(5)
Микропоток характеризует передачу субстанции между соседними частицами среды и пропорционален интенсивности изменения субстанции вдоль координатного направления. Например, составляющая микропотока вдоль оси x определяется как: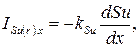 
где kSu – коэффициент субстанциональной проницаемости среды.
Вектор микропотока можно записать как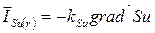 
. (6)
Дата добавления: 2015-06-10; просмотров: 1826;