Математические модели, их свойства и состав
Математическая модель (ММ) представляет собой логическую знаковую конструкцию вида 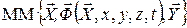 ,включающую уже известные проектные параметры:
,включающую уже известные проектные параметры: 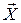 – вектор внутренних параметров,
– вектор внутренних параметров, 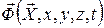 – вектор физических переменных,
– вектор физических переменных, 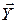 – вектор выходных параметров.
– вектор выходных параметров.
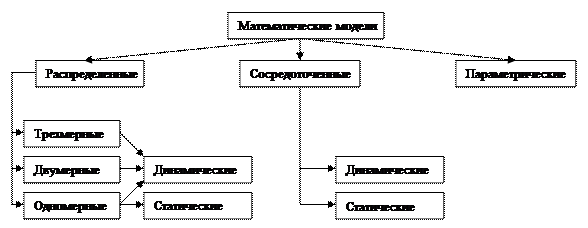
Распределенные ММ отражают процессы, протекающие в пространственной сплошной среде, при этом физические переменные изменяются в зависимости от координат пространства и в каждой отдельной точке принимают свои значения: 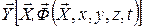 .
.
В зависимости от размерности исследуемого пространства различают одномерные, двумерные и трехмерные модели.
Если модель описывает физический процесс, развивающийся во времени, то ММ является динамической, в противном случае, когда время не влияет на исследуемый процесс, – статической.
ММ представляет собой системы уравнений в частных производных (СУЧП) первого или второго порядка, начальные условия (НУ)(для динамических ММ) и граничные условия (ГУ).
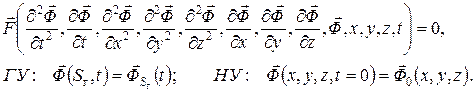 (1)
(1)
Для статических одномерных моделей используются системы обыкновенных дифференциальных уравнений (СОДУ) второго порядка:
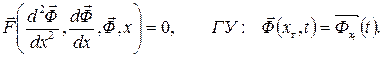 (2)
(2)
Сосредоточенные ММ предполагают осреднение переменных по всей области физической системы, т. е. их независимость от координат пространства.
Динамические сосредоточенные модели представляют собой системы обыкновенных дифференциальных уравнений первого (СОДУ) порядка, дополненные начальными условиями:
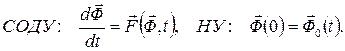 (3)
(3)
Статические модели – это системы алгебраических или трансцендентных уравнений (САУ, СТУ):
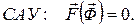
 (4)
(4)
Параметрические ММпредставляют собой аналитически выраженные непосредственные зависимости выходных параметров объекта от внутренних параметров и строятся без использования фундаментальных положений и физических переменных на основе теории планирования и проведения экспериментов с физическими или логическими моделями объектов 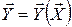 .
.
Дата добавления: 2015-06-10; просмотров: 895;
