Анализ статистических балансовых моделей
Рассмотрим экономическую систему, состоящую из двух объектов. За предшествующий период исполнение баланса характеризуется данными, представленными в табл.2.2. При этом в системе использованы следующие факторы: труд (в человеко-часах) и капиталовложения (в тысячах рублей).
Таблица 2.2
Исполнение баланса производства
| Фактор | Номер объекта | Потребление | Валовый выпуск | |
| и фактора | ||||
| Производство | ||||
| Труд Капиталовложения | - - |
Требуется составить матрицы прямых и полных затрат экономической системы.
Решение. Используя формулу определения коэффициентов прямых затрат 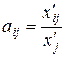 , вычисляем
, вычисляем
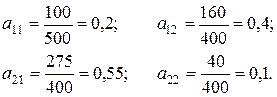
Аналогично определяем коэффициенты прямых затрат факторов, исходя из того, что коэффициент 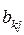 прямых затрат
прямых затрат 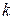 -го фактора для
-го фактора для 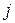 -го объекта равен отношению затрат этого фактора объектом к полному выпуску продукции этим объектом, взятым за прошедший период:
-го объекта равен отношению затрат этого фактора объектом к полному выпуску продукции этим объектом, взятым за прошедший период:
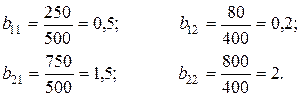
Таким образом, имеем
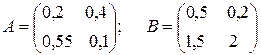 .
.
Далее вычисляем матрицу 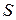 .
.
Так как 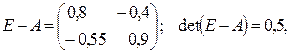 то
то 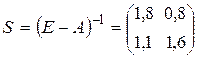 .
.
Вычислим теперь матрицу коэффициентов полных затрат факторов:
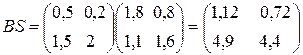 .
.
Задавая значение вектора конечной продукции 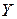 , по формулам (2.5) и (2.8) можем найти показатели плана: валовую продукцию и суммарную потребность системы в факторах.
, по формулам (2.5) и (2.8) можем найти показатели плана: валовую продукцию и суммарную потребность системы в факторах.
Пусть, например, задан вектор 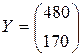 .
.
Тогда 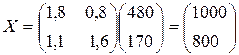 ;
; 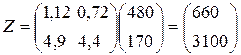 .
.
Отсюда заключаем, что запланированный выпуск конечного продукта может быть достигнут при валовом выпуске объектов 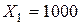 и
и 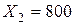 при суммарных затратах труда
при суммарных затратах труда 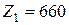 и при затратах капиталовложений
и при затратах капиталовложений 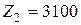 .
.
В народном хозяйстве вырабатывается большое число наименований различных видов и типов продукции. Учесть все их при построении балансовой модели производства часто невозможно из-за отсутствия данных, а также вследствие большого объема технической информации.
Иногда целесообразно проводить укрупнение (объединение) балансовой таблицы. При этом возможно объединение таких видов продукции, которые являются результатом последовательной переработки тех или иных видов сырья (например, железная руда - чугун - сталь - прокат). Такое объединение называется вертикальным. Кроме того, возможно объединение продуктов, сходных по своему экономическому назначению, потребительским свойствам (различные виды топлива, зерна, химикатов и т.п.), именуемое горизонтальным объединением.
После объединения, например, двух объектов экономической системы 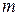 -го и
-го и 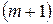 -го коэффициент прямых затрат объединенного объекта
-го коэффициент прямых затрат объединенного объекта
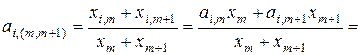
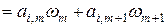 ,
,
где 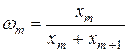 ;
; 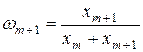 - удельные веса объемов производства отдельных объектов в объеме объединенного объекта.
- удельные веса объемов производства отдельных объектов в объеме объединенного объекта.
Для перехода от детальной таблицы к укрупненной пользуются матрицей агрегирования 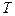 , для которой номер строки i соответствует номеру укрупненного объекта, номер столбца j соответствует номеру исходного объекта:
, для которой номер строки i соответствует номеру укрупненного объекта, номер столбца j соответствует номеру исходного объекта: 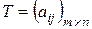 ;
; 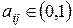 ,
, 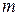 <
< 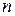 . Например,
. Например, 
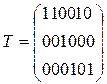 .
.
Данная матрица агрегирования соответствует случаю, когда 1-й объединенный объект включает 1, 2 и 5-й исходные объекты; 2-й объединенный объект включает 3-й исходный объект; 3-й объединенный объекты включает 4-й и 6-й исходные объекты.
Процесс объединения в матричной форме может быть записан следующим образом:
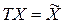 ;
; 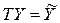 ;
; 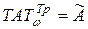 , (2.9)
, (2.9)
где 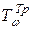 - матрица, полученная из
- матрица, полученная из 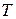 путем транспонирования и замены единичных элементов значениями удельных весов продукции отдельных объектов в соответствующем укрупненном объекте.
путем транспонирования и замены единичных элементов значениями удельных весов продукции отдельных объектов в соответствующем укрупненном объекте.
Тогда на основании уравнения (2.4) и (2.9) будем иметь
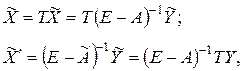
где 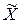 получено при укрупнении результатов расчета по исходной балансовой таблице, а
получено при укрупнении результатов расчета по исходной балансовой таблице, а 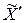 - при расчетах по укрупненной таблице, причем
- при расчетах по укрупненной таблице, причем 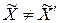 из-за потери информации.
из-за потери информации.
Возникает проблема такого укрупнения, при котором вектор 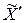 должен как можно меньше отличаться от вектора
должен как можно меньше отличаться от вектора 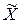 .
.
Дата добавления: 2015-04-21; просмотров: 1258;
