Динамические балансовые модели
Конкретные особенности производства и имеющиеся данные приводят к различным дополнениям и видоизменениям общей схемы построения баланса и решения балансовых уравнений.
Иногда по ряду объектов задаются объемы производства этих объектов, а по ряду других - объемы конечного продукта, т.е. смешанный состав неизвестных в балансовой модели производства (табл.2.3).
Таблица 2.3
Блочно-матричный вид смешанной балансовой модели производства
| Валовый выпуск | Структурная матрица | Конечный продукт |
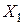
| 
| 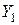
|
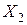
| 
|  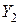
|
Все виды продукции делятся две группы. В первой группе искомыми являются валовые выпуски 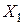 , заданные объемы конечного продукта
, заданные объемы конечного продукта 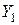 ; во второй группе искомыми являются
; во второй группе искомыми являются 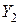 и заданными
и заданными 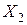 .
.
Запишем в блочно-матричном виде системы балансовых уравнений:
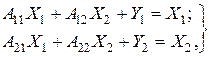 (2.10)
(2.10)
где 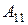 - матрица коэффициентов прямых затрат объектов, по которым заданы конечные продукты;
- матрица коэффициентов прямых затрат объектов, по которым заданы конечные продукты;
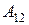 - матрица коэффициентов прямых затрат объектов, по которым заданы конечные продукты, на производство продукции объектов, по которым заданы объемы производства;
- матрица коэффициентов прямых затрат объектов, по которым заданы конечные продукты, на производство продукции объектов, по которым заданы объемы производства;
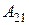 - матрица коэффициентов прямых затрат объектов, по которым заданы объемы производства, на производство продукции объектов, по которым заданы конечные продукты;
- матрица коэффициентов прямых затрат объектов, по которым заданы объемы производства, на производство продукции объектов, по которым заданы конечные продукты;
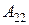 - матрица коэффициентов прямых затрат объектов, по которым заданы объемы производства.
- матрица коэффициентов прямых затрат объектов, по которым заданы объемы производства.
Решение системы (2.10) проводятся в два этапа. Сначала решается первое уравнение и находится вектор 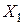 :
:
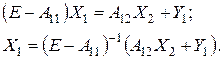
Затем найденный вектор 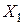 подставляется во второе уравнение и определяется вектор
подставляется во второе уравнение и определяется вектор 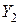 :
: 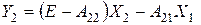 .
.
Рассмотренная статистическая балансовая модель производства характеризует состояние экономики в данный момент и не учитывает динамику развития народного хозяйства. Получаемые средние уровни затрат не отражают многообразия возможных технологий, реализацию достижений технического прогресса. Поэтому на основе межотраслевого баланса нельзя решать задачи экономической динамики, т.е. определять оптимальные темпы и пропорции развития различных отраслей народного хозяйства. На частичное устранение недостатков статических балансовых моделей направлены динамические модели.
По характеру математической модели динамические балансы представляются в виде системы линейных дифференциальных или разностных уравнений.
В качестве примера рассмотрим динамическую модель, позволяющую учитывать капиталовложения в различные объекты экономической системы, а также связь между общими объектами производства в различные периоды.
Обозначим количество продукции 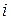 - го объекта, затрачиваемое в данный период на капиталовложения в
- го объекта, затрачиваемое в данный период на капиталовложения в 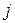 -й объект, через
-й объект, через 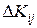 . Номер периода обозначим индексом
. Номер периода обозначим индексом 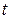 .
.
Тогда основная балансовая система уравнений (2.3) преобразуется в систему
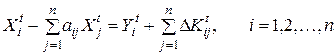 . (2.11)
. (2.11)
Обычно предполагают, что необходимые для объекта капиталовложения пропорциональны приросту продукции объекта, т.е.
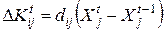 .
.
В результате уравнение (2.11) приводится к виду
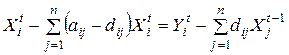 . (2.12)
. (2.12)
Величины 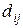 , называемые коэффициентами вложений, позволяют выявить необходимую связь, существующую между периодами. Из системы (2.12), зная общие объемы производства по всем объектам в период
, называемые коэффициентами вложений, позволяют выявить необходимую связь, существующую между периодами. Из системы (2.12), зная общие объемы производства по всем объектам в период 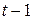 и объемы потребления, можно найти объемы производства в период
и объемы потребления, можно найти объемы производства в период 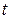 .
.
Такого рода модели учитывают динамику развития экономической системы.
Дата добавления: 2015-04-21; просмотров: 1038;
