Оптимальные траектории. Характеристика оптимальных траекторий

Утверждение, что в кооперативной игре существует равновесное решение, является своего рода контраналогом теоремы Эрроу о невозможности, так как если это утверждение справедливо, то обычно можно построить и функцию общественной полезности. Основополагающей здесь служит теорема Дж. Нэша.

Обозначим множество всех соглашений как A={a,b,c…}. Элементы этого множества — это, например, различные распределения продукции (5.24) или же a={a₁,…,a_m} — это доли дохода, приходящиеся каждому индивиду и т. д. Индивидуальные полезности, как и раньше, определены на альтернативных соглашениях из a; если u_i(a)fu_i(b), то индивид предпочитает соглашение a соглашению b. Каждому соглашению aÎA сопоставляется вектор индивидуальных полезностей u(a)={u₁(a),…,u_m(a)}. Множество всех таких векторов, определенных для каждого соглашения из А, обозначим как S:

S={u(a)|aÎA}.

Обозначим через `u<sub>i</sub> максимальный выигрыш, который индивид i может получить, действуя в одиночку, будем называть этот выигрыш предпосылкой. Предпосылке `u={`u<sub>1</sub>,…,`u_m} соответствует некоторая альтернатива из А, например а. (Для простоты считаем альтернативы, доставляющие одинаковые полезности, неразличимыми.) Предпосылке `u может соответствовать, например, начальное распределение некоторого продукта, имеющегося в объеме X.

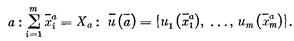
Пусть индивиды пришли к некоторому другому соглашению, например b:

При переходе от соглашения a к соглашению b происходит перераспределение продукта, а также, быть может, изменение его объема, например увеличение: X_b>X_a. Таким образом, предпосылка и может соответствовать вектору индивидуальных полезностей при status quo. Но это не обязательно. Возможна ситуация, в которой никто ничего не получает, если индивиды не сумели договориться о распределении благ. Предпосылка — это максимально возможный выигрыш индивида i в том случае, когда он действует в одиночку, причем не исключена возможность того, что все остальные играют против него. В общем случае этот выигрыш может оказаться и положением status quo и уничтожением и перераспределением всех ресурсов в свою пользу. Выяснение, каково `u<sub>i</sub>, — это специальная и часто очень сложная задача, поиск решения которой ведется методами теории игр. Пусть, например, общество состоит из двух индивидов; у каждого есть набор чистых стратегий c<sub>1</sub> и c<sub>2</sub> и смешанные стратегии y<sub>1</sub> и y<sub>2</sub>; исходы описываются платежными матрицами B<sub>1</sub> и B<sub>2</sub> — для первого и второго индивида соответственно. Имеем, таким образом, биматричную игру с матрицами B<sub>1</sub> и B<sub>2</sub>. Самое большое, на что могут рассчитывать индивиды, действуя в одиночку, это предпосылки `u_i:

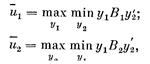
где y' обозначает транспонирование вектора y.

Приведем еще один простой пример, иллюстрирующий понятие предпосылки. Пусть двое рабочих работают в две смены на одном станке. Организация труда индивидуальная; существуют потери времени на пересмену. При такой организации труда месячная зарплата первого и второго рабочих равна x₁^И и x₂^И соответственно, а суммарная зарплата равна X_И=x₁^И+x₂^И. Допустим теперь, что эти рабочие объединились в бригаду нового типа: работают на один наряд, получают единое производственное задание. Если объединение в бригаду оказалось эффективным, то выросла производительность труда (в частности, в результате исчезновения потерь времени на пересмену) и соответственно выросла суммарная зарплата X_d>X_И. Ситуация, соответствующая индивидуальной организации труда, и будет предпосылкой при решении задачи распределения зарплаты X_d: самое меньшее, на что следует соглашаться каждому рабочему,— это его зарплата при индивидуальной организации труда: x_i^И. Полезность этого распределения и будет предпосылкой

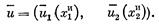
Допустим теперь, что известны множество S и предпосылки и `uÎS. Задача заключается в поиске правила, которое каждой паре (S,`u) ставило бы в соответствие некоторое соглашение, при котором индивиды получали бы полезность u^*:

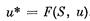
Если S непусто, то такое правило (в отличие от задачи агрегирования индивидуальных предпочтений) всегда существует: можно просто положить u^*=u — каждый «остается при своих». Речь идет, конечно, о правиле, которое улучшило бы положение индивидов. В общем случае и таких правил может оказаться слишком много. Так, в примере с бригадой производственных рабочих любое распределение бригадой зарплаты X_d, такое, что

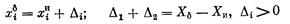
увеличит индивидуальные полезности рабочих (если, конечно, X_d-X_И>0).

Необходимо поэтому сформулировать условия, которым должно удовлетворять разумное правило заключения соглашения. Дж. Нэш сформулировал ряд таких условий; одни из них уточняют понятие разумности соглашения, другие являются гипотезами о функциях полезности.

Условие 1. Все индивидуальные полезности измерены в шкале интервалов, т.е. с точностью до начала отсчета a_i и масштаба bi: преобразование полезности a_i+b_iu_i является допустимым.

Условие 2. Решение — действительное соглашение — не должно зависеть от допустимых преобразований шкал индивидуальных полезностей, т. е. от чисел a_i, b_i. Пусть S' получено из S с помощью допустимых преобразований:

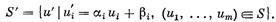
Тогда, если u^*=F(S,`u), то условие 2 содержит требование, чтобы

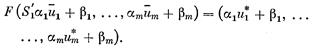
Условие 3. Индивидуальная разумность: для всех i должно выполняться

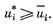
Условие 4. Допустимость:

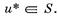
Условие 5. Оптимальность по Парето: в S не существует элемента u^**, отличного от u^*, такого, что u_i^**³u_i^*. Иными словами: после заключения соглашения никто не может улучшить свое положение, не ухудшив при этом положение остальных индивидов.

Условие 6 — независимость от внешних альтернатив: пусть ZÌS. Тогда, если u^*ÎZ и u^*=F(S,`u), должно выполняться u*=F(Z,`u).

Иными словами, при добавлении новых альтернатив (соглашений) старая альтернатива не должна стать решением, если она не была им ранее, при условии, что предпосылки не изменились.

Хотя, так же как и в случае теоремы Эрроу, независимость несвязанных альтернатив не является законом природы, следует все же отметить различие содержания этого условия в формулировках теоремы Эрроу и теоремы Нэша. В последнем случае в модели учитываются результаты отказа от достижения соглашения. Общество из несговорчивых индивидов наказывается тем, что получает только свои предпосылки.

Условие 7 — симметрия: при одинаковом положении в S индивиды должны получать одинаковые выигрыши.

Дж. Нэш доказал теорему, которая действительно удивительна: существует единственная функция F, определенная для всех пар (S,`u), удовлетворяющая условиям 1—7; при этом решением u<sup>*</sup>=F(S,`u) является соглашение, которое максимизирует функцию общественной полезности u₀:

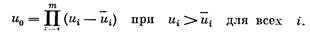
Вернемся к нашему примеру с производственной бригадой. Допустим, что функция полезности денег первого рабочего—это функция Г. Крамера:

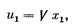
а также любая функция вида 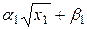при a₁>0 и любых b₁, функция полезности второго рабочего линейна и определяется с точностью до констант a₂ и b₂ (a₂>0):

Введем обозначения:

D=X_d-X_И — прирост суммарной зарплаты при переходе на бригадную организацию труда; z_i — доля рабочего i в этом приросте; x_i^И — зарплата рабочего i при индивидуальной организации труда. Запишем функцию полезности Нэша

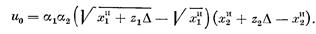(5.5)

Решением, т. е. распределением приработка А, которое удовлетворяет условиям 1—7, будет вектор (z₁,z₂), максимизирующий (5.5) и удовлетворяющий условиям

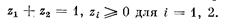(5.6)

Перепишем (5.5) в виде

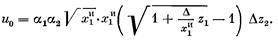
Ясно, что решение не зависит от произвольных постоянных a_i и b_i; в данном случае оно не зависит также от x₂^И. Если отношение D/x₁^И невелико (чаще всего дело обстоит именно так и D/X_И£0.05-0.15), то целевую функцию можно упростить. Имеем

откуда

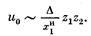
Максимизация этой целевой функции при ограничениях (5.6) эквивалентна задаче: найти z₁ и z₂, такие, что

u₀=z₁z₂®max, z₁+z₂=1, z_i³0, i=1,2.

Сразу получаем, что z_i=1/2. Значит, в первом приближении приработок D следует делить поровну, если дележ должен удовлетворять условиям 1—7. Сразу возникает вопрос: где же здесь личный трудовой вклад каждого рабочего? Личный трудовой вклад каждого рабочего — это предпосылки; приработок, величина которого должна зависеть от величины дополнительно производимой продукции,— это нелинейный эффект кооперации, эффект, который нельзя разложить на сумму индивидуальных эффектов. Попытки разложить этот нелинейный эффект заканчивается неудачей: теория вменения не работает не только на макроуровне, но и на микроуровне.

Можно несколько обобщить полученный результат. Функция Нэша для бригады из m рабочих имеет вид

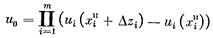
или

Оценим отношения D/x₁^И. Если D=aX_И, где a — процент прироста зарплаты при переходе на бригадную организацию труда, а X_И — средняя зарплата при индивидуальной организации, то D=am`x_И, полагая, что разброс зарплаты невелик, получаем D/x_i^И»am. Рост зарплаты на 100¸150%, конечно, возможен, но все-таки эта ситуация встречается редко (и вызывает сомнения в напряженности норм и эффективности профориентации и расстановки рабочих). Реально в основном a£0.1. Таким образом, если численность бригады не велика (а она должна быть ограничена сверху, так как неосвобожденный бригадир не имеет управленческого аппарата), то am<1. Допустим, что это так. Тогда

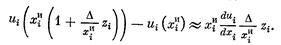
Это дает возможность записать задачу поиска распределения зарплаты, удовлетворяющего условиям 1— 7, в виде

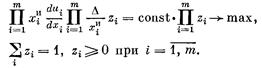
Отсюда следует, что в первом приближении, независимо от формы индивидуальных функций полезности, z_i^*=1/m. Можно показать, что для конкретных индивидуальных функций полезности точка соглашения мало отличается от точки z_i^*=1/m.

Разумеется, теорему Наша нельзя интерпретировать как гарантию существования функции общественной полезности. Выполнение условий 1—7 необходимо проверять в каждом конкретном случае .Сильным является условие 1, по которому все индивиды способны измерить свои индивидуальные полезности в шкале интервалов. В этом, кстати, одно из существенных отличий условий теоремы Нэша от условий теоремы Эрроу. В последней предполагается, что полезность измеряется в порядковой шкале. Если считать способность формулировать свои предпочтения не только в порядковой, но и в количественной шкале признаком разумности, то в теореме Нэша фигурируют более разумные индивиды, чем в теореме Эрроу. Однако в общем случае такой высокой степени разумности для того, чтобы найти приемлемое решение, не требуется. В формулировках основных теорем экономического равновесия (например, в теореме Эрроу-Дебре, в модели В. Л. Макарова) предполагается только, что экономические агенты оценивают свои полезности в порядковой шкале.

Важный результат теории экономического равновесия — установление того факта, что при определенных условиях (например, при отсутствии монополии) оптимальные траектории роста совпадают с равновесными. Этим в значительной степени уменьшается острота проблемы построения единой целевой функции экономики: экономическая система, в которой права принятия решений не сконцентрированы у какой-то группы экономических агентов, а распределены между всеми участниками, способна развиваться оптимально.

Ясная и четкая формулировка условий, при которых существуют или не существуют функции полезности, измеряемые в определенных шкалах, является необходимой предпосылкой для построения функции полезности. Именно поэтому абстрактные аксиомы теории полезности (Дж. фон Неймана и О. Моргенштерна, Л. Сэвиджа, К. Эрроу и др.) имеют непосредственно практическое значение. Противопоставление аксиоматических методов построения функции полезности прямым, эмпирическим, лишено смысла. Получить достаточно адекватную модель целей и поведения экономических агентов можно только на основе сопоставления результатов, получаемых различными путями. По-видимому, единственная область, где обосновано использование экспертных оценок,— это построение функции полезности, но только в том случае, когда эксперты оценивают свои, а не чьи-то, предпочтения. Методы построения функций полезности на основе опросов в настоящее время интенсивно разрабатываются. Получен ряд интересных и имеющих практическую значимость результатов. Но в конечном счете о предпочтениях и целях надо судить не только и не столько по декларациям о намерениях, а по наблюдаемому поведению.