Основные предельные положения теории вероятностей сводятся к следующему.
Первое неравенство Чебышева: если СВ 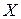 неотрицательна и имеет математическое ожидание, то
неотрицательна и имеет математическое ожидание, то 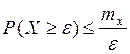 .
.
Второе неравенство Чебышева: если 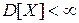 , то вероятность того, что отклонение случайной величины
, то вероятность того, что отклонение случайной величины 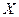 от ее математического ожидания по абсолютной величине меньше положительного числа e, не меньше, чем
от ее математического ожидания по абсолютной величине меньше положительного числа e, не меньше, чем 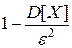 , т.е.
, т.е.
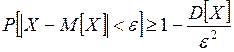 ;
; 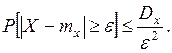
Неравенства Чебышева дают только верхнюю границу вероятности рассматриваемого отклонения, выше этой границы вероятность не может быть ни при каком законе распределения.
Наиболее часто используется вторая форма неравенства.
Теорема Бернулли утверждает устойчивость частоты при постоянных условиях опыта, т.е. при неограниченном увеличении числа опытов  частота события
частота события 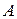 сходится к его вероятности
сходится к его вероятности
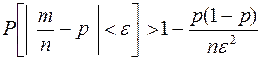 ,
,
где 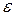 – сколь угодно малое положительное число,
– сколь угодно малое положительное число,
m – количество наступлений события А.
Все формы центральной предельной теоремы (предельных законов распределения) посвящены установлению условий, при которых возникает нормальный закон распределения. Одна из самых простых форм относится к случаю одинаково распределенных слагаемых.
Теорема. Если 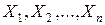 - независимые случайные величины, имеющие один и тот же закон распределения с математическим ожиданием m и диcперсией
- независимые случайные величины, имеющие один и тот же закон распределения с математическим ожиданием m и диcперсией 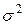 , то при неограниченном увеличении
, то при неограниченном увеличении 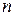 закон распределения их суммы
закон распределения их суммы 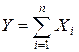 неограниченно приближается к нормальному.
неограниченно приближается к нормальному.
Эта теорема в достаточно широком классе условий справедлива и для неодинаково распределенных слагаемых. Практически центральной предельной теоремой можно пользоваться и тогда, когда речь идет о сумме сравнительно небольшого числа (порядка десяти) случайных величин.
На практике центральная предельная теорема используется в виде двух формул Муавра-Лапласа.
1. Локальная теорема Лапласа (Муавра-Лапласа).
Если число независимых опытов 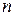 велико (несколько сотен), то
велико (несколько сотен), то
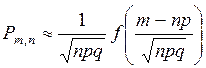 , где
, где 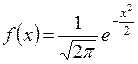 .
.
Вероятность того, что событие 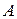 в n опытах произойдет ровно m раз, вычисляется через нормированную плотность нормального закона.
в n опытах произойдет ровно m раз, вычисляется через нормированную плотность нормального закона.
2. Интегральная теорема Лапласа (Муавра-Лапласа).
Если число независимых опытов n велико (несколько сотен), то вероятность появления события 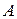 не менее
не менее 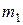 и не более
и не более 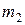 раз определяется по формуле:
раз определяется по формуле: 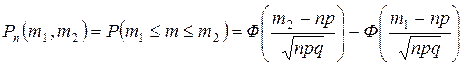 ,
,
где 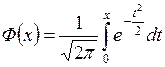 – функция Лапласа.
– функция Лапласа.
Из интегральной теоремы Муавра-Лапласа следует, что вероятность того, что относительная частота 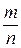 события отклоняется от его вероятности в отдельном испытании
события отклоняется от его вероятности в отдельном испытании 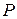 по абсолютной величине не более, чем на
по абсолютной величине не более, чем на 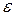 , определяется по формуле
, определяется по формуле 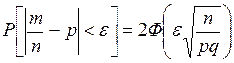 .
.
Примечание. Формула Бернулли, локальная теорема Муавра-Лапласа и формула закона Пуассона дают ответ на один и тот же вопрос, а именно, они определяют вероятность того, что в n независимых испытаниях некоторое событие наступит ровно m раз, если в каждом испытании это событие может наступить с постоянной вероятностью р. По формуле Бернулли получаем точное значение вероятности этого события. Однако из-за вычислительных трудностей эта формула применяется только в случаях, когда число испытаний n невелико.
Если число испытаний будет большим, то используется локальная теорема Муавра-Лапласа, а если, кроме того, вероятность поступления события в отдельном испытании мала, то - формула Пуассона
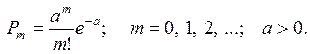
Вероятность искомого события, получаемая по локальной теореме Муавра-Лапласа, оказывается достаточно точной, если число 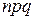 не меньше 20
не меньше 20 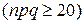 . Если же
. Если же 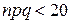 и вероятность р не мала, то для подсчета искомой вероятности нужно обратиться к формуле Бернулли.
и вероятность р не мала, то для подсчета искомой вероятности нужно обратиться к формуле Бернулли.
Формула Пуассона применяется в том случае, когда при большом числе испытаний n вероятность наступления события в каждом испытании весьма мала, а число 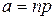 невелико (не больше 10).
невелико (не больше 10).
Система двух случайных величин 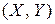 полностью описывается двумерным законом распределения, обычно задаваемым в одной из трех форм.
полностью описывается двумерным законом распределения, обычно задаваемым в одной из трех форм.
1. Ряд распределения. Для системы двух дискретных случайных величин закон распределения удобно задавать в виде прямоугольной таблицы, где по одной стороне откладываются возможные значения одной переменной, по другой - значения второй переменной, а в соответствующих клетках на пересечении столбцов и строк заносятся вероятности совместного появления событий (табл.3.1).
Таблица 3.1
Дата добавления: 2015-04-21; просмотров: 1004;
