Логико-вероятностный метод
ЛВМ возник в результате исследований проблем безопасности сложных систем. С его помощью можно оценить вероятность отказа сложной системы.
ЛВМ относится к аксиоматическим методам принятия решений в условиях стохастической неопределенности. Он позволяет снизить эту неопределенность своим доказательным подходом и результатами экспериментов – вероятностными характеристиками альтернатив.
В пособии ЛВМ рассмотрен на примере решения задачи выбора наиболее надежной информационной системы.
Пусть множество альтернатив – это множество показателей рисков информационных систем (ИС). Требуется найти такую ИС, риск которой минимален.
Под риском системы рассматривается сумма рисков ресурсов, из которых она состоит:
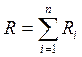 , (5.1)
, (5.1)
где Ri – риск i-го ресурса, n – количество ресурсов. С каждым ресурсом связано множество опасных состояний (ОС), реализация которых приводит к отказу данного ресурса.
В качестве примеров ресурсов ИС могут выступать информационные ресурсы, сервисы, физические или аппаратные ресурсы, программное обеспечение. Одним из примеров информационного ресурса может выступать база данных ИС.
Под риском i-го ресурса понимается сумма рисков, связанных с реализацией опасных состояний данного ресурса:
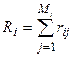 , (5.2)
, (5.2)
где rij – риск реализации j-го опасного состояния i-го ресурса, 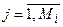 ; Mi – количество опасных состояний i-го ресурса.
; Mi – количество опасных состояний i-го ресурса.
Примерами ОС для ресурса «БД» являются нарушение конфиденциальности информации, полная или частичная потеря информации из-за выхода из строя носителя информации, нарушение доступа.
Под риском реализации j-го опасного состояния i-го ресурса понимается произведение вероятности Pij и стоимости потерь Cij от реализации данного опасного состояния ресурса:
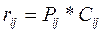 .
.
Таким образом, задачу оценки риска системы можно разбить на следующие этапы:
1. описание структуры ресурсов системы;
2. описание множества опасных состояний ресурсов системы;
3. оценка вероятностей Pij реализации опасных состояний, в том числе, выявление меры влияния угроз на реализацию опасных состояний;
4. оценка стоимости потерь Cij от реализации опасных состояний.
Далее будет рассмотрен этап оценки вероятностей Pij реализации опасных состояний на основе логико-вероятностного метода.
Основные положения логико-вероятностного метода
Логико-вероятностный метод анализа безопасности сложных технических систем был предложен в 70-х годах 20 века
И. А. Рябининым. Основная идея данного метода состоит в сочетании логического и вероятностного подходов при оценке показателей надежности сложных технических, экономических, социальных систем и других систем [6].
В ЛВМ в качестве базовых используются понятия опасного состояния системыи опасности – способности системы переходить в опасное состояние. Описание опасного состояния системы начинается с составления сценария опасного состояния(ОС), который строится с использованием операций дизъюнкция и конъюнкция над инициирующими условиями и событиями.
В качестве инициирующих условий и событий выступают отказы одного или нескольких элементов системы. Каждому элементу системы ставится в соответствие логическая переменная xk ( 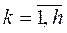 ) с двумя возможными состояниями (например, работоспособности/отказа, готовности/неготовности и т.п.) c заданными вероятностными параметрами этих состояний pk и qk=1-pk.
) с двумя возможными состояниями (например, работоспособности/отказа, готовности/неготовности и т.п.) c заданными вероятностными параметрами этих состояний pk и qk=1-pk.
Сценарий является основой для составления логической функции, или функции алгебры логики (ФАЛ), описывающей опасное состояние системы.
Следующим шагом является преобразование функции алгебры логики к вероятностной функции, которая в дальнейшем используется для получения количественной оценки вероятности реализации опасного состояния.
Таким образом, с одной стороны, метод предоставляет механизм для формализации множества опасных состояний системы, а, с другой стороны, – теоретически обоснованный подход к количественной оценке риска системы.
Для системы, состоящей из различных ресурсов, ЛВМ используется с целью получения количественных оценок вероятностей реализации опасных состояний для каждого вида ресурсов. В свою очередь, каждый ресурс в ЛВМ также рассматривается как отдельная система.
Постановка задачи оценки вероятностей реализации опасных состояний ресурса
Дано:
1. Ресурс с номером i, для которого выделены опасные состояния Sij, 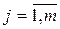 , где m - число возможных состояний.
, где m - число возможных состояний.
2. Структура ОС и вероятности инициирующих событий (угроз) xk , 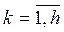 .
.
Требуется найти:
Вероятности Pij реализации опасных состояний Sij, 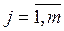 .
.
Алгоритм решения
Шаг 1. Составление сценария опасного состояния Sij.
Шаг 2. Построение функции алгебры логики (ФАЛ) 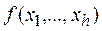 с использованием операций конъюнкция и дизъюнкция на основе сценария опасного состояния Sij.
с использованием операций конъюнкция и дизъюнкция на основе сценария опасного состояния Sij.
Шаг 3. Построение вероятностной функции (ВФ) 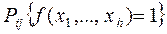 на основе функции алгебры логики.
на основе функции алгебры логики.
Шаг 4. Расчет вероятности Pij реализации опасного состояния с помощью вероятностной функции.
Теоретические основы ЛВМ
В настоящее время математическая логика и теория вероятностей объединяются на основе логико-вероятностного исчисления [7]. При этом предполагается, что теория вероятностей позволяет количественно оценивать надежность или безопасность систем, структура которых описывается средствами математической логики.
Основной проблемой в практическом применении ЛВМ является преобразование произвольных ФАЛ к формам перехода к полному замещению (ФППЗ). Для того чтобы сделать это преобразование стандартным и математически строгим, необходимо обратиться к специальному теоретическому аппарату, основные понятия и теоремы которого будут приведены ниже.
Будем полагать, что каждому элементу системы ставится в соответствие логическая переменная xk , ( 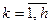 ) с двумя возможными состояниями (работоспособности/отказа, готовности/не готовности и т.п.) c заданными вероятностными параметрами этих состояний pk и qk=1-pk :
) с двумя возможными состояниями (работоспособности/отказа, готовности/не готовности и т.п.) c заданными вероятностными параметрами этих состояний pk и qk=1-pk :

Кроме того, делается предположение, что все события xk являются независимыми в совокупности и что на рассматриваемом интервале времени работы системы исходные параметры законов распределений элементов не изменяются.
Выражение вида 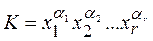 называется элементарной конъюнкцией K ранга r. Выражение вида
называется элементарной конъюнкцией K ранга r. Выражение вида 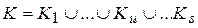 , где
, где 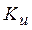 – элементарные конъюнкции различных рангов, называется дизъюнктивной нормальной формой(ДНФ). Если функция
– элементарные конъюнкции различных рангов, называется дизъюнктивной нормальной формой(ДНФ). Если функция 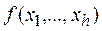 записана в ДНФ, причем ранг каждой элементарной конъюнкции равен n, то такая ДНФ называется совершенной дизъюнктивной нормальной формой(СДНФ).
записана в ДНФ, причем ранг каждой элементарной конъюнкции равен n, то такая ДНФ называется совершенной дизъюнктивной нормальной формой(СДНФ).
Выражение вида 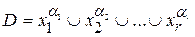 называется элементарной дизъюнкцией ранга r.
называется элементарной дизъюнкцией ранга r.
Две элементарные конъюнкции называются ортогональными, если их произведение равно нулю (пример: 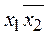 и
и 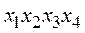 ).
).
ДНФ называется ортогональной дизъюнктивной нормальной формой (ОДНФ), если все ее члены попарно ортогональны.
Бесповторной ДНФ (БДНФ) называется такая ДНФ, в которой каждая логическая переменная встречается ровно один раз.
Правила де Моргана позволяют логическое умножение выразить через отрицание логической суммы инверсий высказываний, а логическую сумму – через отрицание логического произведения инверсных высказывания. В дальнейшем они будут использоваться для приведения ФАЛ к специальному виду:
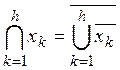 и
и 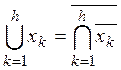
Вероятностной функцией (ВФ) будем называть вероятность истинности ФАЛ:
P(f(x1, x2, …, xh)=1)
Функции алгебры логики, допускающие непосредственный переход к вероятностной функции заменой логических переменных вероятностями, а логических операций соответствующими арифметическими операциями, назовем формами перехода к замещению (ФПЗ).
Формами перехода к полному замещению (ФППЗ) называются ФПЗ, в которых производится замещение одновременно всех логических переменных.
Булевой разностью функции 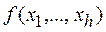 по аргументу xk называется
по аргументу xk называется
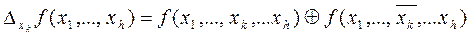 ,
,
где символом « 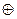 » обозначена логическая операция «сумма по модулю два».
» обозначена логическая операция «сумма по модулю два».
Функция 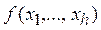 называется монотонной, если для любых наборов (a1, …, ah) и (b1, …, bh), таких, что
называется монотонной, если для любых наборов (a1, …, ah) и (b1, …, bh), таких, что 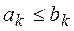 , (k=1,2,…,h) имеет место соотношение f(a1, …, ah)
, (k=1,2,…,h) имеет место соотношение f(a1, …, ah) 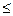 f(b1, …, bh). Далее рассмотрим ряд основных теорем.
f(b1, …, bh). Далее рассмотрим ряд основных теорем.
Теорема 1.Частная производная от вероятности истинности монотонной ФАЛ 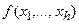 по вероятности истинности аргумента xk численно равна вероятности истинности булевой разности этой функции по аргументу xk:
по вероятности истинности аргумента xk численно равна вероятности истинности булевой разности этой функции по аргументу xk:
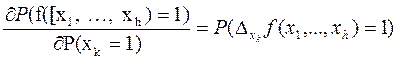 .
.
Теорема 2.Вероятность истинности произвольной ФАЛ, представленной в ОДНФ, равна сумме вероятностей истинности всех ортогональных членов этой ФАЛ:
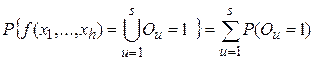 ,
,
где Ou – не только элементарные конъюнкции ОДНФ, но и любые ФАЛ, попарно ортогональные.
Теорема 3.Дизъюнкция ортогональных бесповторных форм в базисе конъюнкция-отрицание является формой перехода к полному замещению.
В настоящее время известно несколько ФППЗ – это совершенная дизъюнктивная нормальная форма (СДНФ), ортогональная дизъюнктивная нормальная форма (ОДНФ) и бесповторные ФАЛ (БФАЛ) в базисе «конъюнкция-отрицание».
Если ФАЛ представлена в ФППЗ, то переход к вероятностной функции осуществляется по следующим правилам:
1. Каждая логическая переменная в ФППЗ заменяется вероятностью ее равенства единице:
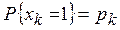 ,
, 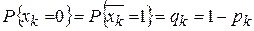 ;
;
2. Отрицание функции заменяется разностью между единицей и вероятностью равенства этой функции единице;
3. Операции логического умножения и сложения заменяются операциями арифметического умножения и сложения.
Составление сценария опасного состояния
Составления сценария опасного состояния ИС можно представить в виде следующей последовательности шагов:
1. выделение конечного события – опасного состояния (отказа),
2. выделение промежуточных событий, приводящих к реализации опасного состояния и получаемых как комбинация двух или более инициирующих событий,
3. выделение инициирующих событий-угроз.
Для представления опасного состояния используется дерево событий или отказов.
На рис. 5.2 представлен пример сценария опасного состояния в виде дерева событий.
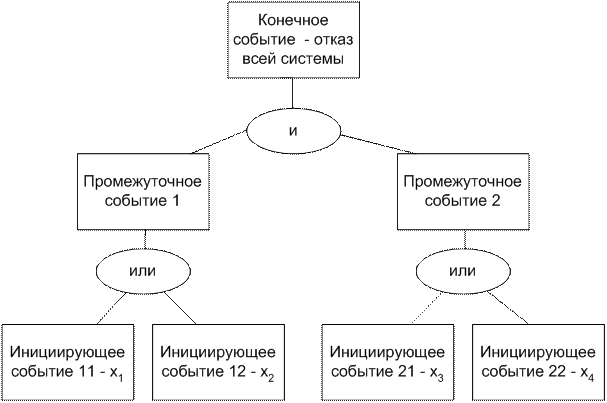
Рис. 5.2. Пример дерева событий для описания опасного состояния системы
Построение функции алгебры логики
С помощью дерева событий составляется функция алгебры логики, описывающая условия перехода системы в опасное состояние.
Для описания условий перехода системы в опасное состояние используется понятие «кратчайший путь опасного функционирования» (КПОФ), под которым понимается конъюнкция минимального набора элементов системы, обеспечивающих вместе переход системы в опасное состояние:
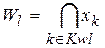 ,
,
где Kwl – множество номеров переменных, соответствующих данному пути.
Условие перехода системы в опасное состояние можно представить в виде дизъюнкции всех имеющихся КПОФ:
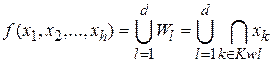 .
.
Пример. Пусть дерево событий имеет вид, представленный на рис. 5.2.
Тогда КПОФ являются: 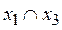 ,
, 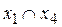 ,
, 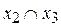 ,
, 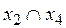 .
.
Условие перехода системы в опасное состояние имеет вид:
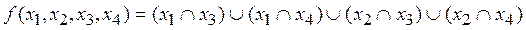 .
.
Построение вероятностной функции
На предыдущем этапе была получена ФАЛ 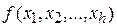 , описывающая опасное состояние системы как дизъюнкцию всех КПОФ. Следующим шагом является преобразование ФАЛ к ФППЗ – СДНФ, ОДНФ или бесповторной ФАЛ в базисе конъюнкция-отрицание (БФАЛ).
, описывающая опасное состояние системы как дизъюнкцию всех КПОФ. Следующим шагом является преобразование ФАЛ к ФППЗ – СДНФ, ОДНФ или бесповторной ФАЛ в базисе конъюнкция-отрицание (БФАЛ).
Построение вероятностной функции на основе ФППЗ осуществляется согласно правилам, описанным выше. Результатом данного этапа является вероятностная функция
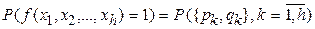
Расчет оценки вероятности реализации опасного состояния
Подставляя значения 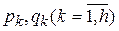 в ВФ, полученную на предыдущем этапе, получаем оценку вероятности реализации опасного состояния Pij.
в ВФ, полученную на предыдущем этапе, получаем оценку вероятности реализации опасного состояния Pij.
Пример
Рассмотрим пример применения ЛВМ для оценки риска реализации опасного состояния «Нарушение конфиденциальности базы данных ИС (БД ИС)».
Шаг 1. Составление сценария опасного состояния ресурса (рис. 5.3).
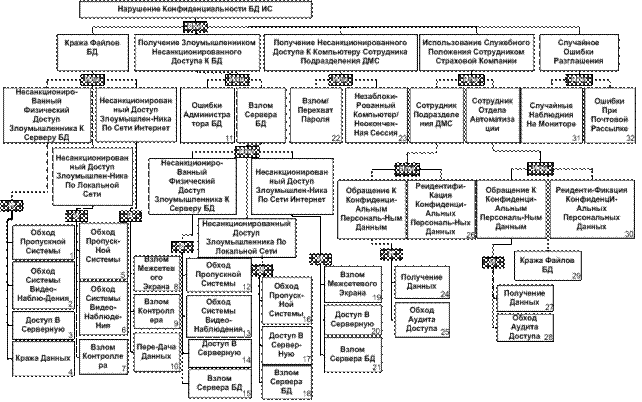 Рис. 5.3. Сценарий ОС «Нарушение конфиденциальности БД ИС»
Рис. 5.3. Сценарий ОС «Нарушение конфиденциальности БД ИС»
Шаг 2. Построение функции алгебры логики.Согласно описанному сценарию, логическая функция принимает вид:
F=X1X2X3X4 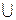 X5X6X7
X5X6X7 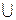 X8X9X10
X8X9X10 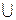 X11
X11 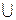 X12X13X14X15
X12X13X14X15 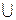 X12X13X14X15
X12X13X14X15 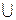
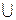 X16X17X18
X16X17X18 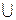
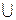 X19X20X21
X19X20X21 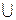 X22
X22 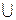 X23
X23 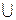 X24X25
X24X25 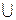 X26
X26 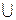 X27X28
X27X28 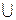 X29
X29 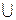 X30
X30 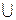 X31
X31 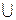 X32
X32
Шаг 3. Построение вероятностной функции.Для расчета итоговой вероятности опасного события функция алгебры логики приводится в базис конъюнкция-отрицание. Таким образом, получаем:
F= 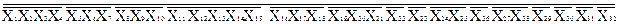
В базисе конъюнкция-отрицание для расчета итоговой вероятности опасного состояния инициирующие события могут быть заменены их вероятностями, полученными на основе статистических данных и экспертных оценок (табл. 5.1):
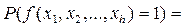 1-((1-p1 p2 p3 p4)(1- p5 p6 p7) (1- p8 p9 p10)
1-((1-p1 p2 p3 p4)(1- p5 p6 p7) (1- p8 p9 p10)
(1- p11 p12 p13 p14 p15) (1- p16 p17 p18) (1- p19 p20 p21)(1-p22) (1-p23)
(1-p24 p25) (1-p26) (1-p27 p28) (1-p29) (1-p30) (1-p31) (1-p32))
Шаг 4. Расчет оценки вероятности реализации опасного состояния.
Таблица 5.1
Вероятности инициирующих событий сценария «Нарушение конфиденциальности БД ИС»
| X1 | X2 | X3 | X4 | X5 | X6 | X7 | X8 | X9 | X10 | X11 | X12 | X13 | X14 | X15 | X16 |
| 0,5 | 0,4 | 0,3 | 0,1 | 0,5 | 0,4 | 0,05 | 0,01 | 0,05 | 0,8 | 0,005 | 0,5 | 0,1 | 0,3 | 0,1 | 0,5 |
| X17 | X18 | X19 | X20 | X21 | X22 | X23 | X24 | X25 | X26 | X27 | X28 | X29 | X30 | X31 | X32 |
| 0,4 | 0,05 | 0,01 | 0,01 | 0,2 | 0,07 | 0,05 | 0,3 | 0,1 | 0,15 | 0,5 | 0,05 | 0,1 | 0,15 | 0,01 | 0,005 |
Таким образом, расчетное значение вероятности реализации опасного состояния P=0,4821. Если потенциальный ущерб оценивается суммой в 3 400 000 рублей, то величина риска определяется как R = P× S, где S – оценка ущерба от реализации опасного состояния, составляет R = 0,4821 × 3 400 000 = 1 639 140 (руб.).
Аналогично оцениваются риски по всем остальным ОС ресурсов ИС. По формуле (5.2) вычисляются риски каждого из ресурсов ИС, а затем по формуле (5.1) – риски самой ИС.
После того, как вычислены величины рисков для всех сравниваемых ИС, в качестве наиболее надежной выбирается та система, для которой величина риска минимальна.
Дата добавления: 2015-05-28; просмотров: 6030;
