Общая постановка однокритериальной статической стохастической задачи принятия решений
Пусть S1, ..., Sl, ..., Sr – набор возможных исходов операции,
X1, ..., Xk, ..., Xt – набор возможных стратегий (альтернатив).
Каждая альтернатива связана с множеством возможных исходов.
Qkl – значение некоторого показателя эффективности операции в случае появления l-того исхода при реализации оперирующей стороной k-ой стратегии.
Hkl – вероятность появления l-ого исхода при реализации k-ой стратегии.
Примерами таких задач могут служить задачи поиска наиболее приемлемого решения в экономических, технических, социальных системах.
При оптимизации решения используют два принципа:
1. «искусственное сведение к детерминированной схеме»,
2. «оптимизация в среднем».
Оба эти принципа представляют собой детерминизацию исходной задачи на разных уровнях влияния стохастических факторов.
Первый связан с детерминизацией на уровне факторов, второй – на уровне показателя эффективности.
При этом перед ЛПР стоят две проблемы. Во-первых, концептуальная, связанная с выбором варианта сведения стохастической задачи принятия решений к детерминированной и выбором критерия оптимальности. Во-вторых, выбор метода решения детерминированной задачи.
Используя первый принцип «искусственное сведение к детерминированной схеме», в задаче все случайные факторы заменяют детерминированными (например, математическим ожиданием М(х)). Этот подход имеет смысл использовать, когда диапазон значений случайной величины мал (как правило, если ведутся грубые расчеты; например, при использовании методов сетевого планирования и управления).
Суть второго принципа «оптимизация в среднем» состоит в переходе от исходного случайного показателя эффективности Q к его некоторой усредненной статистической характеристике.
Пусть операция имеет дискретный характер. В табл. 4.1 представлены возможные значения Qkl некоторого показателя эффективности и вероятности Hkl их появления в операции с t стратегиями и r исходами. Для каждой k-ой стратегии Xk может быть определено математическое ожидание показателя эффективности.
Таблица 4.1
Дискретный случай показателя эффективности
| Исходы стратегии | S1 | S2 | Sl | Sr | Математическое ожидание показателя эффективности | ||
| X1 | H11\Q11 | H12\Q12 | … | H1r\Q1r | F1=M[Q1l]=SQ1lH1l | ||
| … | … | … | … | … | … | … | … |
| Xk | … | …. | ... | Hkl\Qkl | ... | … | |
| … | … | … | … | … | … | … | … |
| Xt | Ht1\Qt1 | Ht2\Qt2 | Htr\Qtr | Ft=M[Qtl]=SQtlHtl |
В качестве оптимальной стратегии Х при «оптимизации в среднем» будет выбрана такая, которая удовлетворяет условию:
F = F(X) = 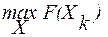 =
= 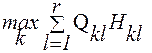 ., k=1,...,t.
., k=1,...,t.
«Оптимизация в среднем» сводит задачу принятия решений в условиях риска к детерминированной, следовательно, для ее решения можно использовать аппарат математического программирования.
Замечание. Первый принцип «искусственное сведение к детерминированной схеме» приводит к тому же результату, что и «оптимизация в среднем» в тех случаях, когда показатель эффективности исхода операции зависит от случайных параметров линейно.
При «оптимизации в среднем» могут быть рассмотрены различные случаи:
1. критерий оптимальности F=M[Q] или Fk=M[M(Qkl)] получен в аналитической форме,
2. критерий оптимальности получен в алгоритмическом виде.
Найденная стратегия Х – такова, что при многократном повторении операции в одинаковых условиях приводит к наилучшему в среднем результату. Всякая другая стратегия даст худший в среднем результат.
Замечание. Выбор той или иной статистической характеристики исходного показателя эффективности Q в качестве критерия оптимальности осуществляется ЛПР.
Дата добавления: 2015-05-28; просмотров: 2028;
