Методы порогов несравнимости
В конце 60-х годов 20 века группа французских ученых во главе с профессором Б. Руа предложила подход к попарному сравнению многокритериальных альтернатив, не основанный на теории полезности. В нем оценка каждой альтернативы является не абсолютной, а относительной (по сравнению с другой альтернативой). Так возник метод ELECTRE (ELimination Et Choix Traduisant la Realite – исключение и выбор, отражающие реальность). В настоящее время разработан ряд методов семейства ELECTRE [4].
Методы ELECTRE направлены на решение задач с уже заданными многокритериальными альтернативами, в них не определяется количественно показатель качества каждой из альтернатив, а устанавливается лишь условие превосходства одной альтернативы над другой.
Эта группа методов характеризуется оригинальным подходом к сравнению альтернатив. Связь между любой парой альтернатив определяется последовательностью бинарных отношений. «Сильным» бинарным отношениям соответствуют бóльшие требования к превосходству одной альтернативы над другой и, следовательно, бóльшее число несравнимых альтернатив. Самым сильным является требование полного доминирования одной альтернативы над другой. Более «слабые» бинарные отношения определяют условия, при которых, несмотря на противоречивые оценки, одна альтернатива лучше другой.
В методах ELECTRE I, II бинарные отношения между альтернативами строятся следующим образом. Каждому из N критериев, имеющих числовые шкалы, ставится в соответствие целое число p, характеризующее важность критерия. Б. Руа предлагает рассматривать p как «число голосов» членов жюри, голосующих за данный критерий.
Выдвигается гипотеза о превосходстве альтернативы a над альтернативой b. Множество I, состоящее из N критериев, разбивается на три подмножества:
I+(a,b) – подмножество критериев, по которым a предпочтительнее b;
I=(a,b) – подмножество критериев, по которым a равноценно b;
I-(a,b) – подмножество критериев, по которым b предпочтительнее a.
Далее формулируется индекс согласия с гипотезой о превосходстве a над b. В методе ELECTRE I этот индекс определяется как отношение суммы весов критериев подмножеств I+ и I= к общей сумме весов:
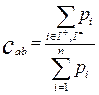 .
.
В методе ELECTRE I определяется индекс несогласия с гипотезой о превосходстве a над b. Для критериев подмножества I-(a,b) находятся разности оценок альтернатив b и a. Индекс несогласия dab определяется на основе самого «противоречивого» критерия – критерия, по которому b в наибольшей степени превосходит a. Чтобы учесть возможную разницу длин шкал критериев, разность оценок b и a относят к длине наибольшей шкалы:
dab = 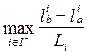 ,
,
где 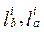 – оценки альтернатив a и b, Li – длина числовой шкалы по i-тому критерию.
– оценки альтернатив a и b, Li – длина числовой шкалы по i-тому критерию.
Укажем очевидные свойства индекса согласия:
1) 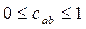 ;
;
2) 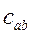 =1, если подмножество I+- пусто;
=1, если подмножество I+- пусто;
3)  сохраняет значение при замене одного критерия на несколько с тем же общим весом.
сохраняет значение при замене одного критерия на несколько с тем же общим весом.
Приведем свойства индекса несогласия:
1) 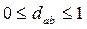 ;
;
2) dab сохраняет значение при введении более детальной шкалы по i-му критерию при той же ее длине.
Введенные индексы используются при построении матриц индексов согласия и несогласия для заданных альтернатив.
В методе ELECTRE I бинарное отношение превосходства задается уровнями индексов согласия и несогласия. Если cab≥c1 и dab≤d1 (где c1, d1 – заданные уровни), то альтернатива a объявляется превосходящей альтернативу b. Уровни c1, d1 позволяют выделить ядро, в которое входят доминирующие и несравнимые элементы.
В методе ELECTRE II гипотеза о превосходстве a над b принимается, если индексы
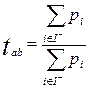 и и
| 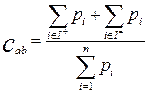
|
достаточно велики, а индекс dab – достаточно мал. Здесь могут быть использованы два типа отношения превосходства – сильное и слабое.
Существуют расширения и модификации этих методов, общим для них является постановка задач и основные этапы решения.
Дано: N критериев со шкалами оценок (обычно количественные), веса критериев (обычно целые числа), альтернативы с оценками по критериям.
Требуется: выделить группу лучших альтернатив.
Основные этапы методов ELECTRE
1. На основании заданных оценок двух альтернатив подсчитываются значения двух индексов: согласия и несогласия. Эти индексы определяют согласие и несогласие с гипотезой, что альтернатива a превосходит альтернативу b.
2. Задаются уровни согласия и несогласия, с которыми сравниваются подсчитанные индексы для каждой пары альтернатив. Если индекс согласия выше заданного уровня, а индекс несогласия — ниже, то одна из альтернатив превосходит другую. В противном случае альтернативы несравнимы.
3. Из множества альтернатив удаляются доминируемые. Оставшиеся образуют первое ядро. Альтернативы, входящие в ядро, могут быть либо эквивалентными либо несравнимыми.
4. Вводятся более «слабые» значения уровней согласия и несогласия (меньший по значению уровень согласия и больший уровень несогласия), при которых выделяются ядра с меньшим количеством альтернатив.
5. В последнее ядро входят наилучшие альтернативы. Последовательность ядер определяет упорядоченность альтернатив по качеству.
Дата добавления: 2015-05-28; просмотров: 2684;
