Прямые методы
Для прямых методов характерна зависимость полезности альтернативы от ее оценок по критериям, которая задается без всяких теоретических оснований, а параметры этой зависимости либо также задаются, либо непосредственно оцениваются ЛПР.
3.2.1. Метод взвешенной суммы. Зависимость имеет следующий вид:
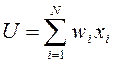 ,
,
где wi – вес (важность) i-го критерия, назначаемый ЛПР; xi – оценка альтернативы по i-му критерию.
Логическим обоснованием метода взвешенной суммы является представление об общей полезности альтернативы как о сумме оценок нескольких независимых критериев. Коэффициенты wi выражают относительную важность оценок критериев.
3.2.2. Мультипликативный метод. Зависимость имеет следующий вид:
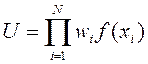 .
.
Чаще всего принимают f(xi)=xi. В некоторых случаях используют метод с зависимостью f(xi)= 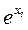 . Путем логарифмирования мультипликативный метод можно свести к суммированию логарифмов оценок, поэтому иногда его объединяют с методом взвешенных сумм. Логическим обоснованием мультипликативного метода является представление об оценках по критериям как о вероятностях достижения определенных показателей качества.
. Путем логарифмирования мультипликативный метод можно свести к суммированию логарифмов оценок, поэтому иногда его объединяют с методом взвешенных сумм. Логическим обоснованием мультипликативного метода является представление об оценках по критериям как о вероятностях достижения определенных показателей качества.
3.2.3. Лексикографическое упорядочивание. В данном методе критерии упорядочиваются по важности, после чего лучшей считается альтернатива, имеющая более высокую оценку по более важному критерию К1 вне зависимости от оценок по прочим критериям. Если оценки по критерию К1 совпадают, альтернативы сравниваются по критерию К2 и т.д.
3.2.4.Метод БОФа. Данный метод предложен в Быстровым Олегом Филаретовичем для сравнительной оценки инвестиционных проектов по множеству показателей [2, с. 54-63].
Целью метода является определение наиболее приемлемого проекта по заданным показателям.
Данный метод может использоваться для оценки любого множества объектов по множеству показателей (критериев) – принятие решений при многих критериях в условиях определенности.
Постановка задачи
Дано:
K – количество объектов, M – количество показателей для сравнения объектов;
R=(R1, R2, … RM) – ранжирование показателей по важности;
|Cij| – матрица значений показателей для объектов 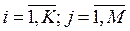 .
.
Требуется упорядочить объекты или выбрать лучший объект.
Описание алгоритма
Метод БОФа состоит из следующих этапов.
1. Отобрать оптимальное количество показателей. Обозначим показатели 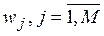 .
.
2. Проранжировать показатели по важности в соответствии с предпочтениями ЛПР. Обозначим ранги показателей 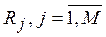 .
.
3. Определить весовые коэффициенты каждого показателя.
Весовые коэффициенты показателей wj определяются по формуле 3.2.1 и затем нормируются по формуле 3.2.2:
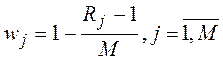
| (3.2.1) |
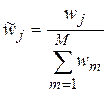
| (3.2.2) |
4. Проранжировать объекты по важности в соответствии с предпочтениями ЛПР по каждому показателю. Обозначим значения показателей для объектов Pji, ранги объектов по показателям 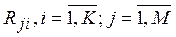 , где K – количество объектов.
, где K – количество объектов.
5. Определить весовые коэффициенты каждого объекта по каждому показателю.
Весовые коэффициенты объектов по каждому показателю 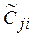 определяются по формуле 3.2.3 и затем нормируются по формуле 3.2.4:
определяются по формуле 3.2.3 и затем нормируются по формуле 3.2.4:
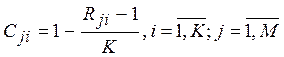
| (3. 2.3) |
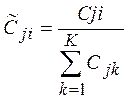
| (3. 2.4) |
Таким образом, для расчета весовых коэффициентов используются отношения порядка между объектами. Однако использованиепорядковой информации может привести к утрате части полезной информации. При необходимости учета количественной информации весовые коэффициенты показателей рассчитываются по формуле 3.2.5, если большие значения показателей предпочтительнее меньших, или по формуле 3.2.6, если меньшие значения предпочтительнее больших. При этом этап 4 (ранжирование объектов по каждому показателю) опускается.
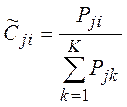
| (3. 2.5) |
Pji – значение показателя j для объекта i.
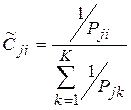
| (3. 2.6) |
6. Рассчитать значения обобщенного показателя для каждого объекта 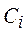 .
.
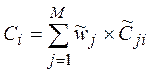
| (3. 2.7) |
7. Проранжировать объекты в соответствии со значениями обобщенных показателей и/или определить лучший объект.
Пример
Требуется выбрать лучший инвестиционный проект для реализации. Для сравнения проектов были выбраны показатели:
NVP (чистый приведенный доход);
IRR (внутренняя норма рентабельности);
PI (индекс прибыльности);
PP (срок окупаемости);
ARR (ср. норма прибыли на инвестиции).
Информация о проектах представлена в табл. 3.1, ранжирование показателей по важности – в табл. 3.2.
Таблица 3.1
Информация о проектах
| Показатели | Проекты | |||
| Проект 1 | Проект 2 | Проект 3 | Проект 4 | |
| NVP (чистый приведенный доход) | 557, 9 | 603,3 | 561,0 | 356,8 |
| IRR (внутренняя норма рентабельности) | 22,7% | 25% | 27,1% | 25,3% |
| PI (индекс прибыльности) | 1,46 | 1,5 | 1,47 | 1,3 |
| PP (срок окупаемости) | 4 года | 4 года | 3 года | 2 года |
| ARR (ср. норма прибыли на инвестиции) | 55% | 55,3% | 45% | 28,3% |
Таблица 3.2
Ранги показателей
| Ранг (Rj) | NPV | IRR | PI | PP | ARR |
| W1 | W2 | W3 | W4 | W5 | |
Таким образом, этап 1иэтап 2 уже выполнены.
Этап 3. Определение весовых коэффициентов показателей и нормирование их значений.
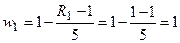 ,
, 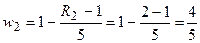 ,
, 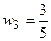 ,
, 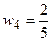 ,
, 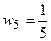 .
.
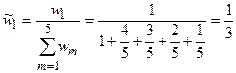 ,
, 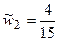 ,
, 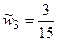 ,
, 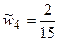 ,
, 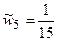 .
.
Этап 4. Ранжирование объектов по каждому показателю.
Проекты сравниваются по каждому показателю и результаты заносятся в таблицу 3.3, Rji – ранг объекта с номером i по показателю с номером j.
Таблица 3.3
Ранги проектов по показателям
| Проект 1 | Проект 2 | Проект 3 | Проект 4 | |
| W1 | R11=3 | |||
| W2 | ||||
| W3 | ||||
| W4 | 3,5 | 3,5 | ||
| W5 |
Этап 5. Определение весовых коэффициентов объектов по каждому показателю и нормирование полученных значений.
Вычислим значения показателя 1 по всем объектам.
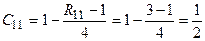 ,
, 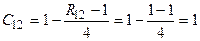 ,
,
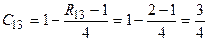 ,
, 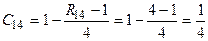 .
.
Пронормируем полученные значения.
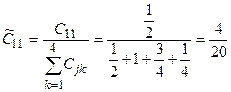 ,
, 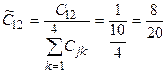 ,
,
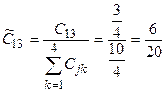 ,
, 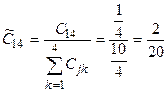 .
.
Значения остальных весовых коэффициентов объектов по показателям вычисляются аналогично.
Этап 6. Расчет значений обобщенного показателя для объектов.
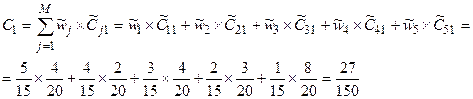
Аналогично вычисляем 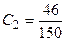 ,
, 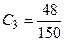 ,
, 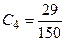 .
.
Этап 7. Таким образом, лучшим является проект 3, на втором месте проект 2, затем идут проекты 4 и 1.
Дата добавления: 2015-05-28; просмотров: 4245;
