Аксиоматические методы
К аксиоматическим методам относится в частности, метод предпочтений и замещений Кини и Райфа [3].
В его основе лежат две центральные идеи – независимость критериев, используемых для сравнения альтернатив, по предпочтению, а также возможность взаимной компенсации значений различных критериев или замещения по ценности. В условиях независимости критериев по предпочтению можно доказать правомерность использования аддитивной линейной функции ценности для сравнения альтернатив. Идея замещения позволяет строить одномерные функции ценности для каждого из критериев.
Постановка задачи
Построить многомерную аддитивную функцию ценности в виде:
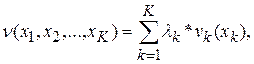
| (3.5.1) |
где νk(xk) – одномерные функции ценности для критериев xk, 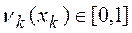 ,
, 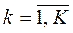 ;
; 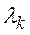 – шкалирующие коэффициенты при одномерной функции ценности vi(xi),
– шкалирующие коэффициенты при одномерной функции ценности vi(xi), 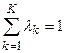 ,
, 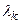 >0.
>0.
Аксиоматика метода
Рассмотрим возможность взаимной компенсации значений различных критериев или возможность «замещения по ценности». Данный вопрос является вопросом личной оценки, для ответа на него необходимо субъективное мнение лица, принимающего решение. Ответы на вопросы о возможности замещения не могут быть правильными или неправильными, так как различные люди могут иметь совершенно разные структуры ценности. Существуют две возможности решения вопроса о замещении по ценности критериев:
1. ЛПР может неформальным образом мысленно сопоставить рассматриваемые возможности замещения,
2. ЛПР может явным образом формализовать свою структуру ценностей и использовать ее для оценивания конкурирующих альтернатив.
Множество критериев Y независимо по предпочтению от дополняющего множества Z тогда и только тогда, когда структура условного предпочтения в пространстве y при фиксированном z’ не зависит от z’.
Более формально, Y не зависит по предпочтению от Z в том и только том случае, если для некоторого z’ выполняется условие:
[(y’,z’) 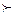 (y’’,z’)]Þ [(y’,z)
(y’’,z’)]Þ [(y’,z) 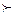 (y’’,z)] при всех z, y’, y’’.
(y’’,z)] при всех z, y’, y’’.
Если ЛПР считает, что множество критериев Y не зависит по предпочтению от дополняющего множества критериев Z, то ему можно будет рекомендовать приложить усилия для структуризации своих предпочтений по y при фиксированном z’, так как не нужно будет повторять эту работу для других уровней z. В этом случае имеет смысл построить функцию ценности vY, определенную для y, не конкретизируя z’. Эта функция должна удовлетворять условию:
(y’,z) 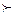 (y’’,z)ÜÞ vY (y’)³ vY (y’’).
(y’’,z)ÜÞ vY (y’)³ vY (y’’).
Критерии X1, X2, …, Xn взаимонезависимы по предпочтению, если каждое подмножество Y этого множества критериев не зависит по предпочтению от своего дополнения.
Теорема о существовании аддитивной функции ценности. Для критериев X1, X2,…, XK, K³3, аддитивная функция ценности 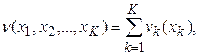 , где vk – одномерная функция ценности (по критерию Xk), существует тогда и только тогда, когда критерии взаимонезависимы по предпочтению.
, где vk – одномерная функция ценности (по критерию Xk), существует тогда и только тогда, когда критерии взаимонезависимы по предпочтению.
Вместо того чтобы использовать аддитивные функции ценности в самой общей форме 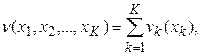 , может оказаться удобным изменить масштаб функции ценности каждого из критериев так, чтобы они изменялись от нуля до единицы. В этом случае мы будем иметь аддитивную функцию вида:
, может оказаться удобным изменить масштаб функции ценности каждого из критериев так, чтобы они изменялись от нуля до единицы. В этом случае мы будем иметь аддитивную функцию вида:
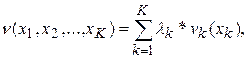
где значения 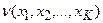 и vk(xk),
и vk(xk), 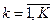 изменяются от нуля до единицы; lk – шкалирующий коэффициент при одномерной функции ценности vk(xk), такой что
изменяются от нуля до единицы; lk – шкалирующий коэффициент при одномерной функции ценности vk(xk), такой что 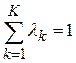 , lk>0.
, lk>0.
Пара (xa, xb) называется эквивалентной по разности ценностипаре (xc, xd), где xa< xb и xc< xd, если, согласившись перейти из xb точно в xa за определенное увеличение Y, мы согласились бы перейти из xd точно в xc за то же самое увеличение по Y. Другими словами, если для любого исходного значения y’ критерия Y мы согласны «заплатить» то же самое количество единиц Y за увеличение по X как от xa до xb, так и от xc до xd, то пара(xa, xb) эквивалентна по разности ценности паре (xc, xd).
Средней по ценности точкой xc интервала [xa, xb] значений критерия X называется такая точка, что пары (xa, xc) и (xc, xb) эквивалентны по разности ценности.
Алгоритм нахождения аддитивной функции ценности
1. Для критерия k ( 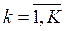 ) построить одномерную функцию ценности νk(xk):
) построить одномерную функцию ценности νk(xk):
1.1. определить наилучшее bk и наихудшее wk возможные значения k-го критерия;
1.2. найти средние по ценности значения k-го критерия m0,5, m0,25, m0,75и т.д.;
1.3. получить одномерную функцию ценности νk(xk).
2. Определить шкалирующие коэффициенты lk критериев ( 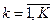 ):
):
2.1. проранжировать шкалирующие коэффициенты lk по степени важности:
lr1 > lr2> …>lrK;
2.2. сравнить профиль (w1, ..., xr1, ..., wK) с профилями x{r2}, x{r3}, ..., x{rK} и найти такие значения 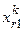 , что
, что
(w1, ... , 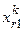 , ..., wK) = v(x{rk} ).
, ..., wK) = v(x{rk} ).
2.3. c использованием условия 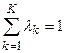 вычислить lk.
вычислить lk.
3. Построить многомерную функцию в виде (3.5.1) и вычислить значения индивидуальных коэффициентов для имеющихся альтернатив.
Рассмотрим подробно каждый этап алгоритма.
Этап 1. Построение одномерных функций ценности.
Шаг 1.1.Определяются наилучшие и наихудшие значения для каждого критерия и заносятся в таблицу.
Таблица 3.4
Наилучшие bk и наихудшие wk значения критериев
| № критерия (k) | 1 | 2 | … | K |
| bk | b1 | b2 | bK | |
| wk | w1 | w2 | wK |
Отметим, что крайние значения критериев могут быть заданы как в виде конкретного значения, так и виде интервала на множестве значений критерия.
Шаг 1.2. Рассмотрим процесс получения средних по ценности значений k-го критерия m0,5, m0,25, m0,75 и т.д.
Вначале нормализуем vk, полагая vk(wk) = 0 и vk(bk) = 1.
Затем эксперт определяет точку, субъективно среднюю по ценности (обозначим ее m0,5) в интервале от wk до bk. Другими словами, эксперт должен найти значение m0,5, для которого vk(m0,5)=0,5, т.е. выяснить, какова та точка разреза, для которой интервалы (wk; m0,5) и (m0,5; bk) эквивалентны по разности ценности.
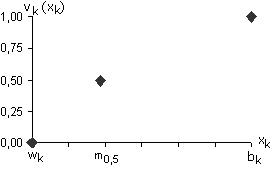
Рис. 3.2. Получение среднего по ценности значения k-го критерия
Затем мы осуществляем ту же самую процедуру для определения точки, средней по ценности в интервале от wk до m0,5 и от m0,5 до bk.
Этот процесс продолжается до тех пор, пока не будет получена требуемая точность или эксперт будет в состоянии проводить сравнения.
После этого найденные точки апроксимируются элементарными функциями (рис. 3.3).
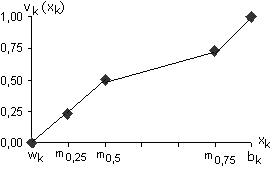
Рис. 3.3. Одномерная функция ценности
Шаг 1.3. В частности, функция vk(xk) может бытьнайдена в виде:
vk(xk)= 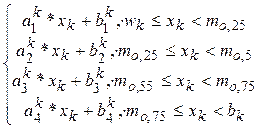
 .
.
А также в виде 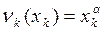 ,
, 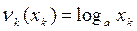 ,
, 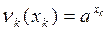 .
.
Аналогично получают одномерные функции ценности по остальным критериям.
Этап 2. Определение шкалирующих коэффициентов критериев.
Шаг 2.1. Эксперты ранжируют критерии по уровню значимости. lr1 > lr2> … >lrK , то есть наиболее важным оказался критерий r1, наименее значимым – rK, 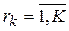 .
.
Шаг 2.2. Набор значений критериев, характеризующих альтернативу Ai, часто называют профилем альтернативыAi. Например, профиль альтернативы есть вектор значений факторов риска (xi1, xi2, …, xiK).
Для удобства изложения введем некоторые специальные обозначения. Пусть K – множество всех номеров критериев. Пусть T – подмножество множества K, 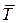 – его дополнение до K, или
– его дополнение до K, или 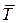 =K\T. Через xT обозначим профиль, в котором компоненты xk равны bk для всех kÎT и wk для kÎ
=K\T. Через xT обозначим профиль, в котором компоненты xk равны bk для всех kÎT и wk для kÎ 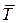 . Таким образом, если, например, T={2,3},то
. Таким образом, если, например, T={2,3},то
xT = x{2,3} =( w1 , b2, b3, w4, w5, … wK).
Так как vk (wk)=0 и vk (bk)=1, то v(xT)= 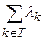 . Если T={2,3}, то многомерная функция ценности v(xT)=l2 +l3. Определим также l(T)=
. Если T={2,3}, то многомерная функция ценности v(xT)=l2 +l3. Определим также l(T)= 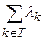 .
.
Отметим, что когда T является одноэлементным множеством {k}, мы имеем v(x{k})=lk =l({k}).
Итак, на шаге 2.1 эксперты проранжировали критерии следующим образом: lr1 > lr2> … >lrK , 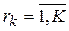 .
.
Теперь будем поочередно сравнивать профиль (w1, .., xr1, .., wK) с профилями x{r2}, x{r3}, .., x{rK}.
Рассмотрим подробнее процесс сравнения двух профилей:
(w1, .. , xr1, .., wr2, wr2+1, .., wK) и x{r2}=(w1, .., w r1, .., br2, wr2+1, .., wK).
Будем изменять уровень xr1, пока не наступит момент безразличия в выборе между альтернативами. Предположим, что это происходит при xr1=с:
(w1, .. , c, .., wr2, wr2+1, .., wK) и x{r2}=(w1, .., w r1, .., br2, wr2+1, .., wK).
Тогда имеем:
v(w1, .. , c, .., wr2, wr2+1, .., wK) = v(w1, .., w r1, .., br2, wr2+1, .., wK) или lr1*vr1 (c) = lr2.
А так как предполагается, что компонента vr1 функции ценности уже построена, то мы можем найти vr1(c) и численно выразить lr1 через lr2.
Таким же образом мы можем определить соотношения между lr1 и lr3, lr1 и lr4, lr1 и lr5, …, lr1 и lrK.
Шаг 2.3. С использованием условия 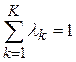 находим значения шкалирующих коэффициентов lk,
находим значения шкалирующих коэффициентов lk, 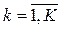 .
.
Этап3. На основании полученных выражений для одномерных функций ценности и найденных значений шкалирующих коэффициентов получим выражение для многомерной функции ценности в виде (3.5.1).
Пример
Для оценки риска при страховании автомобилей страховая компания использует индивидуальные характеристики транспортного средства (ТС) и водителей, допущенных к управлению:
1. Возраст младшего водителя (при наличии нескольких водителей), число целых лет.
2. Стаж вождения наименее опытного водителя (при наличии нескольких водителей), число целых лет.
3. Количество водителей, допущенных к управлению транспортным средством.
4. Возраст транспортного средства, число целых лет.
5. Действительная стоимость транспортного средства на момент оценки риска, тыс. рублей.
6. Цвет транспортного средства. Предлагается использовать 4 группы цветов:
группа 0 – светлые тона не «металлик» (белые, бежевые),
группа 1 – цветные не «металлик»,
группа 2 – темные (черные, синие, темно-зеленые) не «металлик»,
группа 3 – любые цвета с названиями, включающими слова «металлик», серебристые, золотистые.
7. Отсутствие требований выплат (безаварийная эксплуатация). В качестве значений данного фактора предлагается использовать количество лет безаварийной эксплуатации транспортного средства.
Требуется:
1. построить многомерную функцию для оценки риска при страховании автомобиля с помощью метода, предложенного Кини и Райфа;
2. найти значение функции для профиля (возраст водителя 30 лет; стаж 5 лет; 1 дополнительный водитель; возраст ТС 2 года; стоимость 120 тыс. руб.; цвет «металлик»; 0 лет безубыточной эксплуатации).
Исходные данные. По оценкам экспертов были получены крайние значения критериев и занесены в таблицу 3.5.
Таблица 3.5
Наилучшие bi и наихудшие wi значения критериев
| Номер критерия | |||||||
| Наименование критерия | Возраст водителя | Стаж водителя | Число дополнительных водителей | Возраст ТС | Действительная стоимость ТС, тыс. руб. | Цвет ТС | Количество лет безаварийной эксплуатации |
| bi | 30 - 50 | светлый | |||||
| wi | 18; 80 | металлик |
Эксперты проранжировали критерии по уровню значимости следующим образом:
l4 >l5 >l2 >l1 >l7 >l6 >l3 ,
то есть наиболее важным при оценке ожидаемого размера ущерба оказался возраст транспортного средства, наименее значимым – число дополнительных водителей (помимо основного), допущенных к управлению автомобилем.
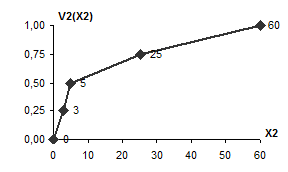
Одномерные функции ценности представлены в таблице 3.6.
Таблица 3.6
Одномерные функции ценности

| 
|
| 1. Возраст водителя | 2. Стаж |

| 
|
| 3. Число дополнительных водителей | 4. Возраст транспортного средства |

| 
|
| 5. Действительная стоимость транспортного средства | 6. Цвет транспортного средства |

| |
| 7. Количество лет безаварийной эксплуатации автомобиля |
При сравнении профилей были получены следующие выражения l1, l2, l3, l5, l6, l7 через l4:
l5 = 0,92l4 ; l2 = 0,83l4 ; l1 = 0,75l4 ; l7 = 0,625l4 ; l6 = 0,5l4 ;
l3 = 0,375l4.
Решение. С использованием условия 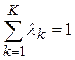 были вычислены весовые коэффициенты критериев: l1 =0,15; l2 =0,166; l3 = 0,075; l4 =0,2; l5 = 0,184; l6 =0,1; l7 = 0,125.
были вычислены весовые коэффициенты критериев: l1 =0,15; l2 =0,166; l3 = 0,075; l4 =0,2; l5 = 0,184; l6 =0,1; l7 = 0,125.
На основании полученных выражений для одномерных функций ценности и найденных значений шкалирующих коэффициентов получим выражение для многомерной функции ценности:
v(x1, x2, x3, x4, x5, x6, x7) =
= 0, 15* 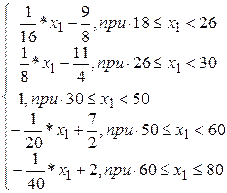
 +0,166*
+0,166* 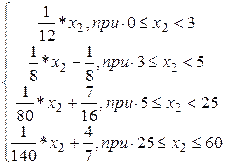

+0,075* 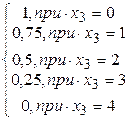 +0,2 *
+0,2 * 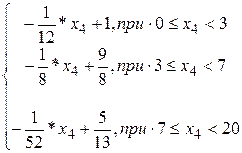

+0,184 * 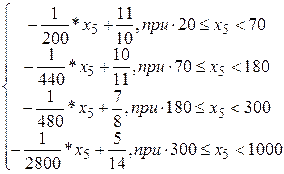
 +0,1*
+0,1* 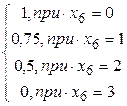
+0,125* 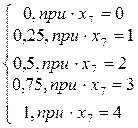
Тогда для профиля (возраст водителя 30 лет; стаж 5 лет; 1 дополнительный водитель; возраст ТС 2 года; стоимость 120 тыс. руб.; цвет «металлик»; 0 лет безубыточной эксплуатации) значение многомерной функции ценности
v(x1, x2, x3, x4, x5, x6, x7) =0,15*1+0,166*0,5+0,075*0,75+0,2*(5/6)+
+0,184*(7/11)+0,1*0+0,125*0=0,5763.
Вопросы и задания
1. Построение рейтинга объектов – это классификация, ранжирование или классификация и ранжирование внутри класса?
2. Где используется предложенная в этом разделе схема парного сравнения альтернатив?
3. Почему поиск Парето-оптимальных альтернатив является начальным этапом задач принятия решений?
4. Есть ли необходимость в нормировании данных при использовании метода взвешенной суммы?
5. Приведите примеры лексикографического упорядочивания альтернатив.
6. Выбрать лучший инвестиционный проект по методу БОФа. Для сравнения проектов выбраны следующие показатели:
- W1 – объем инвестиций, млн. дол.;
- W2 – годовой оборот проекта, млн. дол.;
- W3 – годовой объем чистой прибыли, млн. дол.;
- W4 – срок окупаемости проекта, лет;
- W5 – риск потери инвестиций.
При сравнении проектов важно учесть, что для показателей W1, W2, W3 большие значения предпочтительнее меньших, для показателя W4 меньшие значения предпочтительнее больших, а показатель W5 имеет качественную шкалу.
Таблица 3.7
Исходные данные для сравнения инвестиционных проектов
| Проекты | W1 (объем инвестиций, млн. дол.) | W2 годовой оборот проекта, млн. дол.) | W3 (годовой объем чистой прибыли, млн. дол.) | W4 (срок окупаемости проекта, лет) | W5 (риск потери инвестиций) |
| Проект 1 | 7,8 | 5,5 | Н | ||
| Проект 2 | 1,08 | 1,65 | 0,585 | 2,5 | Н |
| Проект 3 | 1,8 | 4,55 | 0,66 | О | |
| Проект 4 | 3,9 | 0,825 | ОН | ||
| Проект 5 | 1,138 | 1,3 | 1,5 | В | |
| Проект 6 | 0,66 | 0,39 | 2,5 | ОВ | |
| Проект 7 | 0,11 | 0,754 | 0,13 | 2,2 | О |
| Проект 8 | 9,1 | 20,4 | 2,6 | 6,5 | В |
| Проект 9 | 1,1 | 5,2 | 0,585 | 2,75 | В |
«О» – риск отсутствует, «ОН» – очень низкий риск, «Н» – низкий риск, «В» – высокий риск, «ОВ» – очень высокий риск.
Для сравнения проектов по показателю «Риск потери инвестиций» используется порядковая шкала: лучшему значению показателя ставится в соответствие ранг 1, следующему значению ставится в соответствие ранг 2 и т.д. Если несколько проектов имеют одинаковое значение показателя «Риск потери инвестиций», то ранги проектов вычисляются следующим образом. Рассмотрим вариант 1. Проект 1 имеет низкий риск потери инвестиций, проекты 5 и 9 имеют высокий риск потери инвестиций. Тогда проекту 1 в соответствие ставится ранг 1, а проекты 5 и 9 будут иметь одинаковые ранги 2.5, поскольку они разделили 2 и 3 места по этому показателю: 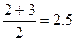 .
.
7. Построить кривые безразличия для оценки альтернатив по критериям «цена» - «качество».
8. Сравнить альтернативы ВУЗ 1, ВУЗ 2, ВУЗ 3 с помощью метода Электра, установив индексы согласия и несогласия. Исходные данные представлены в табл. 3.8.
Таблица 3.8
Исходные данные для сравнения ВУЗов
| № | Критерий | ВУЗ 1 | ВУЗ 2 | ВУЗ 3 |
| Лидирующая роль руководства | 47,1 | 46,2 | 53,9 | |
| Политика и стратегия в области качества | 29,4 | 26,1 | 24,0 | |
| Оценка персонала | 68,9 | 72,1 | 73,7 | |
| Партнерство и ресурсы | 91,4 | 87,7 | 98,4 | |
| Процессы, осуществляемые в ВУЗах | 29,6 | 25,6 | 36,8 | |
| Удовлетворенность потребителями качеством услуг | 47,6 | 38,3 | 51,6 | |
| Удовлетворенность персонала | 62,6 | 62,3 | 65,8 | |
| Оценка общества |
9. Построить функцию ценности для трех критериев, используя аксиоматический метод предпочтений и замещений. Минимальные значения критериев (10, 0, 20), максимальные (20, 50, 60). Все три критерия ориентированы положительно («больше» - «лучше»). Средние по ценности значения для первого критерия (15, 17, 19), второго (5, 10, 20), третьего(50, 53, 57). Первый критерий важнее второго, второй важнее третьего. Профили (17, 0, 20) и (10, 50, 20) равноценны. Профили (10, 10, 20) и (10, 0, 60) также равноценны. Сравнить профили (19, 5, 53) и (10, 10, 30).
Дата добавления: 2015-05-28; просмотров: 2734;
