Методы компенсации

Идея компромисса, уравновешивания по полезности оценок различных критериев, достаточно широко известна. Впервые она была изложена Б. Франклином, где он замечает, что при сравнении трудно одновременно держать в голове все достоинства и недостатки каждой из альтернатив. Поэтому он выписывает в два отдельных списка достоинства и недостатки альтернативы, после тщательного анализа определяет, какой недостаток (или их совокупность) можно считать эквивалентной определенному достоинству (или их совокупности), после чего вычеркивает их из списка.

Переход от сравнения качеств по различным критериям к сравнению альтернатив может быть осуществлен различными путями.

3.3.1.Точки и кривые безразличия. На рис. 3.1 дан пример кривых безразличия для двух критериев оценки альтернатив. Точки p₁, p₂, p₃ называют исходными. Построение кривой безразличия k_i осуществляется следующим образом:

а) выбирается исходная точка p₁(x₁,y₁), где x₁, y₁ – значение критериев X, Y в данной точке;

б) выбирается приращение d по критерию X (положительное или отрицательное) и определяется x₂=x₁+d;

в) определяется значение y₂ по критерию Y такое, что точка p₁’(x₂, y₂) эквивалентна по полезности точке p₁(x₁, y₁);

г) по найденным точкам проводится кривая безразличия.

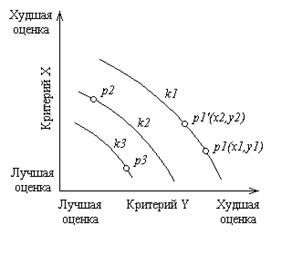
Рис. 3.1. Пример кривых безразличия

Если в многокритериальном пространстве построены поверхности безразличия, то сравнение альтернатив крайне просто, поскольку поверхности (или исходные точки) можно упорядочить по полезности. Так, точка p₂ на рис. 3.1 предпочтительнее p₁.

3.3.2.Методы сравнения разностей оценок альтернатив. Во многих методах принимается как очевидный порядок, при котором нужно сначала оценить полезность альтернативы, а уже потом сравнивать альтернативы между собой. Между тем существует группа методов, в которых принят совсем иной порядок: альтернативы сначала сравниваются покритериально, а уже потом осуществляется общее сопоставление всех достоинств и недостатков каждой из них.

Пусть (x₁, x₂, ..., x_N), (y₁, y₂, ..., y_N) – оценки альтернатив x и y по N критериям. Тогда альтернатива x предпочтительнее, чем альтернатива y, если

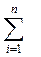j_i[U_i(x_i)-U(y_i)] ≥ 0,

где U_i – функция полезности для i-го критерия, j_i – функция, определяющая влияние разностей оценок альтернатив по i-му критерию на результат сравнения двух альтернатив.