Методы экспертных измерений
Характер произведенных экспертных измерений необходимо принимать во внимание при проведении процедур экспертного оценивания, выработке и принятии управленческих решений, определении коллективных решений. От экспертов требуется однозначное понимание того, что именно и в какой шкале они оценивают, чтобы избежать ситуаций, в которых оценка одного и того же показателя, связана с различными предпосылками.
Если эксперт должен оценить значение количественного показателя, он может это сделать, указав соответствующее численное значение, либо интервал, в котором, по его мнению, лежит значение оцениваемого показателя.
При коллективной экспертной оценке значения показателя, указанные экспертами, либо усредняются, либо обрабатываются с помощью других специальных методов, например, методов экспертных измерений.
2.2.1. Методы получения количественных экспертных оценок. К методам получения количественных экспертных оценок относятся:
Непосредственная количественная оценка, которая используется как при определении значения показателя, измеряемого количественно, так и в случае, когда надо оценить степень сравнительной предпочтительности различных объектов.
Заранее необходимо условиться, что, скажем, большее значение оценки соответствует более предпочтительному альтернативному варианту. Иногда количественную оценку сравнительной предпочтительности объектов целесообразнее производить в баллах, используя специально разработанные балльные шкалы.
Метод средней точки, который используется, когда альтернативных вариантов достаточно много. Если через f(а1) обозначим оценку первого альтернативного варианта значения показателя, относительно которого определяется сравнительная предпочтительность объектов, через f(а2) – оценку второго альтернативного варианта, то далее эксперту предлагается подобрать третий альтернативный вариант а3, оценка которого f(а3) расположена в середине между значениями f(а1) и f(а2) и равна [f(а1)+f(а2)]/2. При этом в качестве первого и второго альтернативных вариантов целесообразно выбирать наименее и наиболее предпочтительные альтернативные варианты.
Далее эксперт указывает альтернативный вариант а4, значение которого f(а4) расположено посередине между f(а1) и f(а2), и альтернативный вариант а5 значение которого f(а5) расположено посередине между значениями f(а2) и f(а3)
Процедура завершается, когда определяется сравнительная предпочтительность всех участвующих в экспертизе альтернативных вариантов. Этот метод может быть использован также при экспертной оценке численных значений показателей, имеющих количественный характер.
Метод численных оценок.Метод состоит из следующих этапов:
1. Для каждой альтернативы определяется вектор оценочных характеристик.
2. Каждая оценочная характеристика формируется и нормируется.
3. Эксперт дает свою оценку важности каждой характеристики.
При этом количество экспертов должно быть больше одного (в общем случае – m).
Оценка выставляется по шкале от 0 до 1. Данные заносятся в таблицу следующего вида:
Таблица 1.3
Исходные данные для определения весов характеристик
| Оценочная характеристика | Эксперты | |||
| ... | m | |||
| k1 | v11 | v1m | ||
| k2 | ||||
| … | vij | |||
| kn | vn1 | vnm |
Здесь ki – i-я характеристика, vij – вес (значимость) i-ой характеристики, назначаемый j-тым экспертом.
4. Затем определяется вес каждой характеристики по формуле:
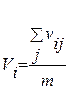
где Vi – средний вес i-ой характеристики.
5. Расчет ценности альтернатив производится по формуле:
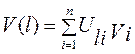 ,
,
где V(l) –ценность l-ой альтернативы;
Uli – нормированное числовое значение i-характеристики l-ой альтернативы;
Vi – средний вес i-той характеристики.
2.2.2. Методы получения качественных экспертных оценок. Экспертная классификация. Этот метод целесообразно использовать, когда необходимо определить принадлежность оцениваемых альтернативных вариантов к установленным и принятым к использованию классам, категориям, уровням, сортам и т. д. (далее — классы). Он может быть использован и тогда, когда конкретные классы, к которым должны быть отнесены оцениваемые объекты, заранее не определены. Может быть заранее не определено и число классов, на которое производится разбиение оцениваемых объектов. Оно может быть установлено лишь после завершения процедуры классификации.
После завершения процедуры последовательного предъявления оцениваемых альтернативных вариантов эксперту может быть предъявлен результат его оценки в виде распределения всех оцененных им альтернативных вариантов по классам.
На этом этапе эксперту, как правило, предоставляется возможность, исходя из общего результата классификации, внести коррективы в данные им оценки.
Если проводится коллективная экспертиза, то результаты экспертной классификации, указанные каждым из экспертов, обрабатываются с целью получения результирующей коллективной экспертной оценки.
Усреднение экспертных оценок. Пусть Y1, Y2,...,Yn – совокупность оценок экспертов, «выставленных» одному объекту экспертизы (например, одному из вариантов стратегического развития фирмы), Z1, Z2,...,Zn – второму (другому варианту такого развития).
Как сравнивать эти совокупности? Очевидно, самый простой способ – по средним значениям. А как вычислять средние? Известны различные виды средних величин: среднее арифметическое, медиана, мода, среднее геометрическое, среднее гармоническое, среднее квадратическое. Обобщением нескольких из перечисленных является среднее по Колмогорову. Для чисел X1, X2,...,Xn среднее по Колмогорову вычисляется по формуле
G{(F(X1)+F(X2)+...F(Xn))/n},
где F – строго монотонная функция, G – функция, обратная к F. Так, если F(x)=x, то среднее по Колмогорову – это среднее арифметическое, если F(x)=ln x, то среднее геометрическое, если F(x)=1/x, то среднее гармоническое, если F(x)=x2, то среднее квадратическое. С другой стороны, такие популярные средние, как медиана и мода, нельзя представить в виде средних по Колмогорову.
При допустимом преобразовании шкалы значение средней величины, очевидно, меняется. Но выводы о том, для какой совокупности среднее больше, а для какой – меньше, не должны меняться. Осуществляется поиск вида средних величин, результат сравнения которых устойчив относительно допустимых преобразований шкалы.
Пусть f(X1, X2,...,Xn) – среднее по Колмогорову. Пусть среднее по первой совокупности меньше среднего по второй совокупности:
f(Y1, Y2,...,Yn) < f(Z1, Z2,...,Zn).
Для устойчивости результата сравнения средних необходимо, чтобы для любого допустимого преобразования g из группы допустимых преобразований в соответствующей шкале было справедливо также неравенство
f(g(Y1), g(Y2),..., g(Yn)) < f (g(Z1), g(Z2),..., g(Zn)),
т.е. среднее преобразованных значений из первой совокупности также было меньше среднего преобразованных значений для второй совокупности. Причем сформулированное условие должно быть верно для любых двух совокупностей Y1, Y2,...,Yn и Z1, Z2,...,Zn и любого допустимого преобразования g. Только такими средними можно пользоваться при анализе мнений экспертов и иных данных, измеренных в рассматриваемой шкале.
Метод парных сравнений представляет собой одну из самых широко используемых экспертных процедур для определения относительных весов объектов, сравниваемых по качественному признаку. Для определения количественных оценок объектов a1,...,an необходимо их сравнение друг с другом. Простейшим видом сравнения являются парные сравнения. Эксперту поочередно предъявляются пары объектов, и он должен каждый раз установить, какой из предъявленных ему объектов предпочтительнее по рассматриваемому признаку. Принято считать, что порядок предъявления эксперту пар объектов не имеет значения, так как не влияет на результаты парных сравнений. Полученную в результате парных сравнений информацию нужно использовать для вычисления количественных оценок объектов.
Аналогичная проблема определения оценок возникает и тогда, когда сравниваемые между собой объекты характеризуются некоторым набором количественных признаков, для которых не удается разработать удовлетворительный общий показатель. Сравнивая два таких объекта, можно по каждому признаку сразу указать, какой из объектов предпочтительнее, однако суждение о предпочтительности объекта по совокупности признаков в большинстве случаев может высказать только эксперт.
Оценивание объектов на основе их парных сравнений можно сформулировать либо как задачу детерминированную, либо как задачу вероятностную. В первом случае полагают, что высказывания эксперта о предпочтении не изменятся, если те же пары объектов будут предъявлены ему повторно, так как у него имеются на этот счет вполне определенные суждения. Во втором случае суждения эксперта считают подверженными случайным изменениям, вводится понятие вероятности предпочтения одного объекта другому; при этом подразумевается возможность многократного сравнения объектов.
Рассмотрим только детерминированную задачу парных сравнений. Рассмотрим случай, когда парные сравнения проводятся единственным экспертом. Результат парных сравнений n объектов можно представить в виде матрицы A=|aij|, где aij=1, если ai предпочтительнее aj, и 0 – в противном случае (aii=0), где ai и aj – сравниваемые объекты (ничейный вариант не рассматривается).
Если предпочтения эксперта последовательны (транзитивны), то в качестве весов объектов естественно принять суммы элементов соответствующих строк матрицы A.
Пример
| Объекты | a1 | a2 | a3 | a4 | a5 | Сумма | gi |
| a1 | 0.4 | ||||||
| a2 | 0.3 | ||||||
| a3 | 0.2 | ||||||
| a4 | 0.1 | ||||||
| a5 | 0.0 |
В данном случае a1 f a2 f a3 f a4 f a5 (знак «f» используется для обозначения отношения предпочтения). Разделив суммы элементов строк на сумму элементов всей матрицы, получим относительные веса объектов:
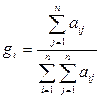
| (2.2.1) |
Если предпочтения эксперта непоследовательны, то суммы элементов строк матрицы парных сравнений не образуют строгого порядка и полученные по формуле (2.2.1) оценки относительных весов не всегда могут быть использованы для упорядочения объектов по предпочтительности. В такой ситуации можно поступить двояко: либо ограничиться полученными неточными оценками, либо попытаться улучшить оценки относительных весов объектов.
Матрицей A задается ориентированный полный граф без петель и встречных дуг, такой граф часто называют турниром (или круговым турниром), так как он может отображать результаты спортивных состязаний, где все команды (или спортсмены) встречаются друг с другом один раз, причем результатом каждой встречи может быть только выигрыш или поражение. За выигрыш команда получает очко, за поражение – ничего (нуль). Сумма элементов i-й строки итоговой таблицы турнира равна количеству побед, одержанных i-й командой. Если две команды набрали равное количество очков, то либо обе команды признаются одинаково сильными, либо они сравниваются по дополнительному показателю для определения наиболее сильной из них. Более сильной может считаться, например, команда, выигравшая встречу между ними. Иногда более сильной считают команду, выигравшую больше встреч у сильных противников, или команду, проигравшую меньше встреч слабым соперникам. Наиболее распространен способ ранжирования на основе определения числа очков каждой команды, учитывающий силу побежденных ею команд.
Обозначим через f(k) вектор, полученный на k-м шаге алгоритма, компоненты которого характеризуют силу команд, k = 1..N. Число очков, которое получит каждая команда на (k+1)-ом шаге равна сумме fi(k), где i – выигранные ей команды, т.е. можно записать f(k)=A·f(k-1), где A – матрица парных сравнений. До начала состязаний все команды считаются равными по силе, поэтому начальный вектор f(0) есть вектор-столбец, каждая компонента которого равна единице. Выполнение алгоритма заканчивается, когда все компоненты вектора f будут различны, веса gi в этом случае считаются аналогично.
Пример
| Объекты | a1 | a2 | a3 | a4 | a5 | Сумма | gi |
| a1 | 0.3 | ||||||
| a2 | 0.1 | ||||||
| a3 | 0.2 | ||||||
| a4 | 0.3 | ||||||
| a5 | 0.1 |
Соответствующая таблица:
| Объекты | f1 | f2 | f3 | f4 | f5 | f6 | f7 | f8 | f9 |
| a1 | |||||||||
| a2 | |||||||||
| a3 | |||||||||
| a4 | |||||||||
| a5 |
Видно, что при k = 4 уже наблюдается строгое ранжирование, которое при дальнейшем увеличении шага только возрастает.
Для .k-го шага значение f(k) можно представить:
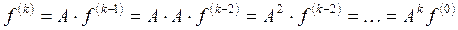 , то есть i-я компонента вектора f(k) есть сумма элементов i-й строки матрицы Ak.
, то есть i-я компонента вектора f(k) есть сумма элементов i-й строки матрицы Ak.
Ранжирование альтернативных вариантов. Достаточно распространенной процедурой является также непосредственное ранжирование экспертом по предпочтительности оцениваемых альтернативных вариантов.
В этом методе эксперту предъявляются отобранные для сравнительной оценки альтернативные варианты, но желательно не более 20-30 для их упорядочения по предпочтительности.
Если альтернативных вариантов больше, то целесообразно использование соответствующих модификаций метода ранжирования.
Например, ранжированию альтернативных вариантов может предшествовать их разбиение на упорядоченные по предпочтению классы с помощью метода экспертной классификации.
Ранжирование сравниваемых объектов эксперт может осуществлять различными способами. Приведем два из них.
В соответствии с первым эксперту предъявляется весь набор альтернативных вариантов, и он указывает среди них наиболее предпочтительный. Затем эксперт указывает наиболее предпочтительный альтернативный вариант среди оставшихся и т.д., пока все оцениваемые альтернативные варианты не будут им проранжированы.
При втором способе эксперту первоначально предъявляются два альтернативных варианта или больше, которые ему предлагается упорядочить по предпочтениям.
Если эксперту первоначально предлагается несколько альтернативных вариантов для упорядочения по предпочтениям, то он на этом этапе может воспользоваться первым способом ранжирования.
После проведения первоначального ранжирования эксперту последовательно предлагаются новые, еще не оцененные им альтернативные варианты. Эксперт должен определить место вновь предъявленного альтернативного варианта среди проранжированных ранее.
Процедура завершается после предъявления и оценки последнего альтернативного варианта.
Метод векторов предпочтений. Этот метод чаще используется при необходимости получения коллективного экспертного ранжирования. Эксперту предъявляется весь набор оцениваемых альтернативных вариантов и предлагается для каждого альтернативного варианта указать, сколько, по его мнению, других альтернативных вариантов превосходит данный.
Эта информация представляется в виде вектора, первая компонента которого – число альтернативных вариантов, которые превосходят первый, вторая компонента – число альтернативных вариантов, которые превосходят второй, и т. д.
Если оценивается 10 альтернативных вариантов, то вектор предпочтений может выглядеть так:
( 3 , 7 , 0 , 4 , 8 , 6 , 1, 9, 5, 2).
Если в векторе предпочтений каждое число встречается ровно один раз, то экспертом указано строгое ранжирование альтернативных вариантов по предпочтениям.
В противном случае полученный результат не является строгим ранжированием и отражает затруднения эксперта при оценке сравнительной предпочтительности отдельных альтернативных вариантов.
Этот метод может быть применен и в случае, когда у эксперта имеются затруднения при использовании других методов оценки сравнительной предпочтительности альтернативных вариантов.
Дискретные экспертные кривые. Если целью является разработка прогнозов или анализ динамики изменения показателей, характеризующих объект выработки и принятия управленческого решения, то целесообразно воспользоваться дискретными экспертными кривыми.
При построении дискретной экспертной кривой определяется набор характерных точек, в которых наблюдается или ожидается смена тенденции изменения значений показателя от рассматриваемого параметра, а также значения показателя в характерных точках.
Участки между характерными точками могут быть соединены отрезками прямой линией (в случае линейности) и экспертными кривыми (в случае нелинейности). Определение результирующей коллективной экспертной оценки, более надежно для дискретных экспертных кривых.
Использование экспертных кривых позволяет более наглядно и надежно представить различные сценарии развития ситуации, что часто бывает необходимым при разработке прогнозов.
Вопросы и задания
1. Какому типу шкал соответствует шкала рейтинга компьютерной безопасности фирм?
2. Как согласовать мнения экспертов при оценке важности характеристик альтернатив?
3. Приведите примеры критериев для всех типов шкал.
Дата добавления: 2015-05-28; просмотров: 4519;
