Множество Парето. Классификация ЗПР в условиях определенности

Общей частью методов принятия решений при многих критериях является отыскание множества Парето-оптимальных альтернатив из всего множества альтернатив. Рассмотрим ЗПР в условиях определенности – множество исходов совпадает с множеством альтернатив.

Пусть для оценивания исходов используется N критериев, причем большее значение критерия предпочтительнее меньшего. Тогда каждый исход (и альтернатива) будет характеризоваться вектором значений критериев (x₁, x₂, …, x_N).

Вектор (x₁, x₂, …, x_N) содержит полную информацию о ценности (полезности) этого исхода для ЛПР, и сравнение любых двух исходов заменяется сравнением их векторных оценок.

Векторная оценка x=(x₁, x₂, …, x_N) доминирует по Парето векторную оценку 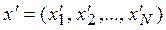(обозначение 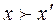), если для всех 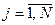выполняется неравенство 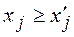и хотя бы для одного индекса j неравенство является строгим.

Векторная оценка 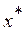называется Парето-оптимальной, если не существует такой векторной оценки x, что .

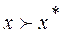Аналогично для исходов.

Альтернатива A₁ доминирует над альтернативой A₂, (обозначение 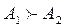), если A₁ не хуже, чем A₂ по всем критериям, а как минимум по одному критерию лучше, или если векторная оценка исхода A₁ доминирует по Паретовекторную оценку исхода A₂.

Альтернатива считается оптимальной по Парето, если нет альтернатив, доминирующих над ней.

Множество недоминируемых альтернатив образует множество Эджворта-Парето (Э-П).

Задача выделения множества Э-П обычно рассматривается как предварительная. За ней следует наиболее существенный этап принятия решений.

Различные методы принятия решений при многих критериях отличаются способом перехода к единой оценке полезности альтернатив. Можно выделить ряд групп таких методов.

В методах первой группы (прямые методы) зависимость общей полезности альтернативы от оценок по отдельным критериям известна заранее. Чаще всего используется вид зависимости, при котором определяются численные показатели важности критериев (веса), умножаемые на оценки по критериям (метод взвешенной суммы оценок критериев).

Во второй группе методов (методы компенсации) пытаются уравновесить (скомпенсировать) оценки одной альтернативами оценками другой, чтобы найти, какие оценки лучше. По идее, это наиболее простой метод, при котором человек выписывает достоинства и недостатки каждой из альтернатив и, вычеркивая попарно эквивалентные достоинства (недостатки), изучает то, что осталось.

В третьей группе (методы порогов несравнимости) задается правило сравнения двух альтернатив, при котором одна альтернатива считается лучше другой (например, оценки первой по большинству критериев лучше). В соответствии с заданным правилом альтернативы делятся (попарно) на сравнимые (одна лучше другой, либо эквивалентные) и несравнимые. Измеряя отношение сравнимости, получаем разное число пар сравнимых альтернатив.

В четвертой группе (аксиоматические методы) определяется ряд свойств, которым должна удовлетворять зависимость общей полезности альтернативы от оценок по отдельным критериям. Эти свойства (называемые аксиомами) проверяются путем получения информации от лиц, принимающих решение. В соответствии с этой информацией делается вывод о той или иной форме зависимости.