ROC-анализ

В классическом виде ROC-анализ позволяет решить задачу разделения множества альтернатив на два класса [13].

Широкое применение он нашел в медицине, например, для диагностики заболеваний. Также метод может использоваться для оценки кредитоспособности физических лиц, для определения группы риска клиентов страховой компании.

Далее рассмотрим метод на примере задачи классификации клиентов страховой компании по трем группам риска (ГР). Классификация необходима для назначения страхового тарифа при заключении договоров добровольного медицинского страхования.

Метода ROC-анализа позволяет установить числовой порог (в виде количества баллов, набранных по анкете), при котором ошибка отнесения клиента к определенной группе будет стремиться к минимуму.

В качестве критериев принадлежности к группе могут использоваться:

1. количество обращений за амбулаторно-поликлинической помощью за определенный период,

2. расходы на медицинское обслуживание за определенный период.

Например, если выбран второй критерий, то к первой группе риска относятся те люди, расходы на медицинское обслуживание которых за определенный период не превысят суммы S₁, ко второй группе – суммы S₂, к третьей группе – все остальные (S₁<S₂).

Аналогично задаются группы риска с учетом количества обращений.

Исходной информацией для определения пороговых значений первой и второй групп риска являются результаты обработки анкет (в виде итогового количества баллов) и сведения о группе риска для выборки из N человек.

Постановка задачи

Дано:

1. Требования страховой компании к 3 группам риска:

1 ГР : R<R₁, 2 ГР : R<R₂, 3 ГР : R≥R₂,

где R – количество обращений к врачу или стоимость медицинского обслуживания в течение года, предшествующему моменту страхования;

R₁, R₂ – ограничения на значения R для первой и второй группы риска.

2. Данные по выборке клиентов СК. Для i-того клиента, 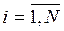, N – количество человек в выборке, известно:

­ r_i, - значение величины R для i-того клиента;

­ значения шкалы G_i= 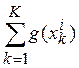, где g(x_kⁱ) – шкальная функция для фактора риска x_k , .

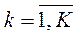Требуется найтипороговые значения шкалы для первой и второй группы риска s₁ и s₂, при которых ошибка отнесения человека к первой и второй группе риска минимальна:

s₁={h_j: 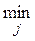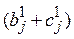} (2.3), s₂={h_j: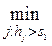 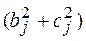} (4.2.1)

{h_j} – множество значений шкалы G_i для выборки из N клиентов СК (множество пороговых значений), j – номер порогового значения, , , ;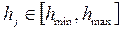

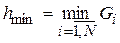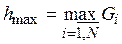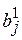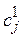, – количество ложноположительных и ложноотрицательных прогнозов для j-того порогового значения, полученных при поиске порогового значения для 1 ГР;

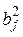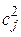, – количество ложноположительных и ложноотрицательных прогнозов для j-того порогового значения, полученных при поиске порогового значения для 2 ГР. А также оценить качество шкалы G= 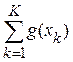, на основе которой принимается решение.

Алгоритм решения

I. Определение порогового значения s₁ для первой группы риска.

1. Вводим гипотезу:

Если значение шкалы G_i<h_j, то человек относится к 1 ГР (исход положительный).

Если значение шкалы G_i≥h_j, то человек не относится к 1 ГР (исход отрицательный).

2. Вводим определения для следующих 4 групп:

A – истинноположительная группа – люди, которых тест отнес к 1 ГР, действительно к ней относятся (прогноз положительного исхода подтвердился);

B – ложноположительная группа – люди, которых тест отнес к 1 ГР, но они к ней не относятся (прогноз положительного исхода не подтвердился);

С – ложноотрицательная группа – люди, которых тест не отнес к 1 ГР при условии, что они к ней относятся (прогноз отрицательного исхода не подтвердился);

D – истинноотрицательная группа – люди, которых тест не отнес к ГР, и они на самом деле к ней не относятся (прогноз отрицательного исхода подтвердился).

3. Проверяем гипотезу для всех пороговых значений 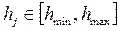. Для этого рассчитываются количество человек, попавших в каждую из групп:

, , ;

, , ;

, , ;

, , .

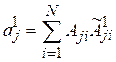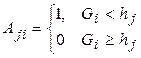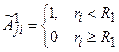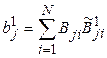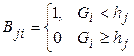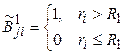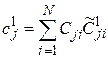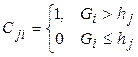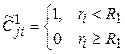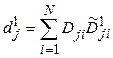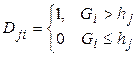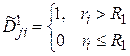4. Определяем пороговое значение по формуле (4.2.1).

5. Строим график характеристической кривой. Для этого введем параметры чувствительность и специфичность:

, .

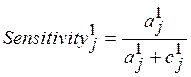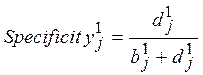Чувствительность представляет собой долю людей, которых тест отнес к 1 ГР, среди всех относящихся к ней для текущего порогового значения g_j.

Специфичность представляет собой долю людей, которых тест не отнес к 1 группе среди всех не относящихся к ней для текущего порогового значения g_j.

Для всех возможных пороговых значений 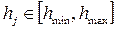отображаем на графике зависимость Sensivity(1-Specificity). Данная кривая называется характеристической кривой и используется для оценки качества используемой шкалы G= 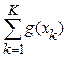при классификации с точки зрения первой группы риска. Чем ближе площадь под кривой к единице, тем качественнее шкала. Пример графика ROC-кривой представлен на рис. 4.1.

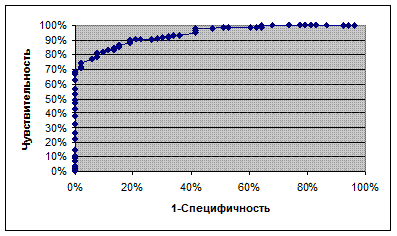
Рис. 4.1. График ROC-кривой

II. Определение порогового значения s₂ для второй группы риска.

При определении группы риска сначала проверяется принадлежность к 1 группе. При этом мы допускаем, что результат теста на принадлежность человека к 1 группе может быть ошибочным. При проверке принадлежности человека ко 2 группе риска мы должны также снизить количество результатов, при которых человек, относящийся к 1 группе риска, мог быть отнесен к третьей. С учетом этого замечания алгоритм примет следующий вид.

1. Вводим гипотезу:

Если значение шкалы G_i<h_j, то человек относится к 2 ГР (исход положительный).

Если значение шкалы G_i≥h_j, то человек не относится к 2 ГР (исход отрицательный).

2. Вводим определения для следующих 4 групп:

A – истинноположительная группа люди, которых тест отнес ко 2 ГР, и они действительно относятся к 1 или 2 ГР.

B – ложноположительная группа – люди, которых тест отнес ко 2 ГР, но они не относятся к 1 или 2 группе (то есть относятся к третьей группе).

С – ложноотрицательная группа – люди, которых тест не отнес ко 2 ГР при условии, что они относятся к 1 или 2 группе.

D – истинноотрицательная группа – люди, которых тест не отнес ко 2 ГР, и они на самом деле не относятся к 1 или 2 группе (то есть относятся к 3 группе).

3. Проверяем гипотезу для всех пороговых значений 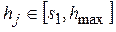. Для этого рассчитываются количество человек, попавших в каждую из групп:

, , ;

, , ;

, , ;

, , .

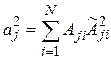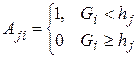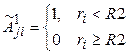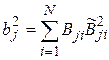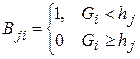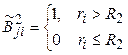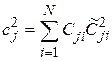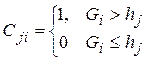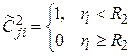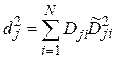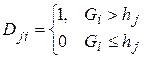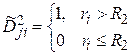4. Определяем пороговое значение по формуле (4.2.1).

5. Для 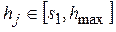строим график характеристической кривой и оцениваем качество шкалы для классификации с точки зрения второй группы риска.

Замечание 1. При выборе пороговых значений следует обратить внимание также на значения чувствительности и специфичности, соответствующие каждому пороговому значению. Рассмотрим процесс выбора порогового значения для 1 ГР.

Для страховой компании (СК) важно:

1. чтобы была высока чувствительность, то есть с помощью анкеты мы должны достаточно хорошо выявлять людей, относящихся к 1 группе риска,

2. чтобы была высока специфичность, то есть доля людей, которых мы не отнесли к 1 группе среди всех не относящихся к ней.

Причем второе условие важнее первого, так как при снижении чувствительности в 1 группу не попадет некоторое количество в действительности относящихся к ней людей. При этом для них договор страхования будет заключен на более выгодных для СК условиях. То есть здесь отсутствует риск финансовых потерь для СК.

При снижении специфичности возрастает риск финансовых потерь для СК, так как возрастает доля людей, попавших в 1 группу риска, но в действительности не относящихся к ней. Следовательно, в качестве порогового значения лучше использовать число, при котором значение специфичности будет приемлемо для СК.

Замечание 2. Данный метод позволяет постоянно уточнять значения пороговых значений по мере накопления статистических данных.

Вопросы и задания

1. Дайте определение задачи принятия решений в условиях неопределенности.

2. В чем суть различий между фиксированными стохастическими и неопределенными факторами?

3. В чем суть различий между неопределенными факторами стохастической и нестохастической природы?

4. Объясните термин «природные неопределенности».

5. Сформулировать задачу принадлежности к классу, используя терминологию ROC-анализа.

6. Как связаны между собой «риск» и «неопределенность»?