Принятие решений в условиях стохастической неопределенности, когда проведение экспериментов невозможно
Учет неопределенных факторы, закон распределения которых неизвестен, базируется на формировании специальных критериев, на основе которых принимаются решения – критерии Вальда, Сэвиджа, Гурвица и Байеса-Лапласа.
Модель проблемной ситуации имеет вид:
< U, V, W >,
где U={ui} – множество стратегий (решений),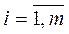 
;
V={vj} – множество состояний природы,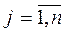 
;
W=|wij| – матрица решений, элемент матрицы wij содержит доходы (или потери) от выбора стратегии ui при реализации состояния природы vj.
Требуется найти оптимальную стратегию.
5.2.1 Критерий Вальда.В соответствии с критериемВальда (критерий крайнего пессимизма)в качестве оптимальной выбирается стратегия, гарантирующая выигрыш не меньший, чем «нижняя цена игры с природой»:
.
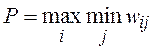Правило выбора решения в соответствии с критерием Вальда можно интерпретировать следующим образом: матрица решений W дополняется еще одним столбцом из наименьших результатов wir каждой строки. Выбрать надлежит тот вариант, в строке которого стоит наибольшее значение wir этого столбца.
Выбранное таким образом решение полностью исключает риск. Это означает, что принимающий решение не может столкнуться с худшим результатом, чем тот, на который он ориентируется. Какие бы условия vj не встретились, соответствующий результат не может оказаться ниже P. Это свойство заставляет считать критерий Вальда одним из фундаментальных. Поэтому в технических задачах он применяется как сознательно, так и неосознанно. Однако в практических ситуациях излишний пессимизм этого критерия может оказаться очень невыгодным.
Применение этого критерия может быть оправдано, если ситуация, в которой принимается решение, характеризуется следующими обстоятельствами:
о вероятности появления состояния природы vj ничего не известно;
с появлением состояния vj необходимо считаться;
реализуется лишь малое количество решений;
не допускается никакой риск.
5.2.2. Критерий Байеса-Лапласа. Критерий Байеса-Лапласа в отличие от критерия Вальда, учитывает каждое из возможных следствий всех вариантов решений:
.
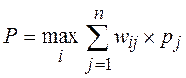Соответствующее правило выбора можно интерпретировать следующим образом: матрица решений W дополняется еще одним столбцом, содержащим математическое ожидание значений каждой из строк. Выбирается тот вариант, в строках которого стоит наибольшее значение wir этого столбца.
Критерий Байеса-Лапласа предъявляет к ситуации, в которой принимается решение, следующие требования:
вероятность появления состояния vj известна и не зависит от времени;
принятое решение теоретически допускает бесконечно большое количество реализаций;
допускается некоторый риск при малых числах реализаций.
5.2.3. Критерий Сэвиджа. В соответствии с критерием Сэвиджа в качестве оптимальной выбирается такая стратегия, при которой величина риска принимает наименьшее значение в самой неблагополучной ситуации:
.
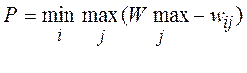Здесь величину P можно трактовать как максимальный дополнительный выигрыш, который достигается, если в состоянии vj вместо варианта ui выбрать другой, оптимальный для этого внешнего состояния, вариант.
Соответствующее критерию Сэвиджа правило выбора следующее: каждый элемент матрицы решений W вычитается из наибольшего результата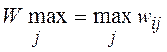 
соответствующего столбца. Разности образуют матрицу остатков (рисков). Эта матрица пополняется столбцом наибольших разностей wir. Выбирается тот вариант, в строке которого стоит наименьшее значение.
5.3.4. Критерий Гурвица. Согласно критерию Гурвицавыбирается такая стратегия, которая занимает некоторое промежуточное положение между крайним пессимизмом и оптимизмом:
,
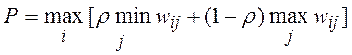где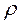 
– коэффициент пессимизма, выбираемый в интервале [0,1].
Правило выбора согласно этому критерию следующее: матрица решений Wij дополняется столбцом, содержащим средние взвешенные наименьшего и наибольшего результатов для каждой строки. Выбирается тот вариант, в строках которого стоят наибольшие элементы wr этого столбца.
При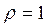 
критерий Гурвица превращается в критерий Вальда (пессимиста), а при 
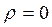– в критерий азартного игрока. Отсюда ясно, какое значение имеет весовой множитель 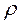. В технических приложениях правильно выбрать этот множитель бывает так же трудно, как правильно выбрать критерий. Поэтому чаще всего весовой множитель 
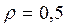принимается в качестве средней точки зрения.
Критерий Гурвица предъявляет к ситуации, в которой принимается решение, следующие требования:
о вероятности появления состояния природы vj ничего неизвестно;
с появлением состояния vj необходимо считаться;
реализуется лишь малое количество решений;
допускается некоторый риск.
Общие рекомендации по выбору того или иного критерия дать затруднительно. Однако отметим следующее: если в отдельных ситуациях не допустим даже минимальный риск, то следует применять критерий Вальда; если определенный риск вполне приемлем, то можно воспользоваться критерием Сэвиджа. Можно рекомендовать одновременно применять поочередно различные критерии. После этого среди нескольких вариантов, отобранных таким образом в качестве оптимальных, приходится волевым решением выделять некоторое окончательное решение.
Такой подход позволяет, во-первых, лучше проникнуть во все внутренние связи проблемы принятия решений и, во-вторых, ослабляет влияние субъективного фактора. Кроме того, в области технических задач различные критерии часто приводят к одному результату.
Пример
Обоснование состава ремонтной бригады. На предприятии решается вопрос о создании ремонтной бригады. Основываясь на применении критериев Вальда, Лапласа, Сэвиджа и Гурвица, определить наиболее целесообразное число членов бригады. Исходные данные сведены в таблице 5.2, в ячейках которой занесены доходы при разных вариантах (стратегиях). x – стратегия – число членов бригады; R – состояние природы – количество станков, которые могут потребовать ремонта.
Таблица 5.2
Исходные данные
| x\R | ||||
1. Критерий Вальда.Справа дописывается столбец минимумов по строкам.
| x\R |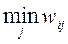 
| ||||
Тогда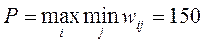 
. Таким образом, при данных условиях рациональным решением будет x=2.
2. Критерий Лапласа.Рассмотрим ситуацию, когда все состояния природы равновероятны. В этом случае критерий примет вид:
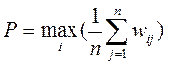
| x\R |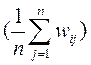 
| ||||
Тогда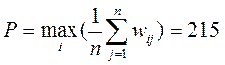 
. Таким образом, наилучшим решением будет x=2.
3. Критерий Сэвиджа. Построим матрицу рисков. Ее элементы определяются по формуле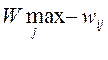 
, где 
.
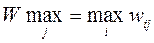| x\R |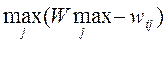 
| ||||
| 300-50=250 | |||||
|
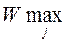
Тогда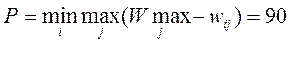 
. Оптимальная стратегия согласно критерию Сэвиджа x=3.
4. Критерий Гурвица. В отличие от примененных выше «жестких» критериев, критерий Гурвица является «гибким», так как позволяет варьировать «степень оптимизма-пессимизма». Таким образом, этот критерий устанавливает баланс между случаями крайнего оптимизма или пессимизма, путем введения коэффициента веса r.
Применим данный критерий к нашим исходным данным, полагая r =0.5.
| x\R |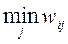
| 
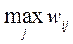
| P | ||||
Таким образом,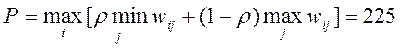 
. Оптимальная стратегия x=2.
Дата добавления: 2015-05-28; просмотров: 2195;