Методы получения оценок альтернатив и критериев на основе результатов парных сравнений

5.4.1. Метод Уэя. Метод собственных векторов Уэя основывается на данных матрицы парных сравнений:

,

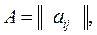
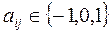где а_ij = -1 означает превосходство параметра x_j над параметром х_i, a_ij=0 – равноценность x_i и x_j , а_ij = 1 – превосходство параметра х_i над х_j.

Ввиду неудобства работы с отрицательными числами матрицу парных сравнений можно превратить в неотрицательную матрицу:

,

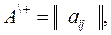
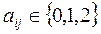где числа 0,1,2 имеют аналогичные значения.

Сложив числа по каждой из строк матрицы, будем иметь числовые характеристики важности параметров, а разделив их на общую сумму – получим весовые коэффициенты параметров:

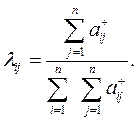
Недостатком этой формулы является то, что она учитывает важность «ничейных» (равноценности х_i и х_j ) и «проигрышных» (когда x_j превосходит x_i) сравнений. Если устранить этот недостаток, то весовыми коэффициентами по сути являются координаты собственного вектора, соответствующего максимальному характеристическому числу матрицы парных сравнении.

5.4.2. Метод Коггера. В этом методе в качестве вектора весов берется решение уравнения:

,

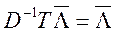где 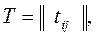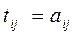при i =j и 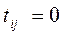при i ≠j;

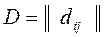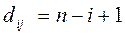, при i =j и 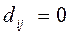при i ≠j, 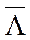–вектор весов.

Преимуществом метода является то, что он менее трудоемок в вычислительном отношении, чем процедура получения собственного вектора матрицы парных сравнений.