Принятие решений в условиях концептуальной неопределенности на основе МАИ Саати
Основная идея метода анализа иерархий (МАИ) Саати [1, 9] заключается в том, что проблема исследования декомпозируется на отдельные части и представляется в виде иерархии. При этом происходит структурирование и упрощение проблемы. Иерархия содержит на верхнем уровне цель, на нижележащих уровнях – подцели и критерии. Результатом работы метода являются значения многомерной функции, построенной для данной иерархии. Значения данной функции для объектов позволяют сравнивать их в смысле достижения цели.
Метод состоит из следующих этапов:
1. формирование иерархии;
2. получение оценок объектов, весовых коэффициентов критериев и подцелей для всех уровней иерархии;
3. оценка однородности суждений эксперта;
4. расчет интегральных оценок объектов.
Формирование иерархии
Построение иерархии начинается с очерчивания проблемы исследования. Далее строится собственно иерархия, включающая цель, расположенную в ее вершине, промежуточные уровни, содержащие подцели и, возможно, критерии, а также объекты, формирующие самый нижний иерархический уровень (рис. 5.4). Уровней может быть сколько угодно.
 |
Рис. 5.4. Пример 4-уровневой иерархии
Получение оценок объектов, весовых коэффициентов критериев
и подцелей
Для формализации знаний эксперта по поводу сравнительной важности расположенных на одном уровне элементов иерархии относительно вышележащего элемента иерархии используется специальная 9-балльная шкала, предложенная автором метода
(табл. 5.3).
Правомочность этой шкалы доказана теоретически при сравнении со многими другими шкалами [1, с. 30]. При использовании указанной шкалы лицо, принимающее решение, (ЛПР), сравнивая два элемента иерархии в смысле их вклада в достижение подцели или цели, расположенной на вышележащем уровне иерархии, должен поставить в соответствие этому сравнению число в интервале от 1 до 9 или обратное значение чисел. В тех случаях, когда трудно различить столько промежуточных градаций от абсолютного до слабого предпочтения или этого не требуется в конкретной задаче, может использоваться шкала с меньшим числом градаций. В пределе шкала имеет две оценки: 1 – элементы равнозначны; 2 – предпочтение одного элемента над другим.
Таблица 5.3
Шкала для парного сравнения подцелей, критериев и объектов
| Степень значимости | Определение | Объяснение |
| Одинаковая значимость | Два действия вносят одинаковый вклад в достижение цели | |
| Некоторое преобладание значимости одного действия над другим (слабая значимость) | Существуют соображения в пользу предпочтения одного из действий, однако эти соображения недостаточно убедительны | |
| Существенная или сильная значимость | Имеются надежные данные или логические суждения для того, чтобы показать предпочтительность одного из действий | |
| Очевидная или очень сильная значимость | Убедительное свидетельство в пользу одного действия перед другим | |
| Абсолютная значимость | Свидетельства в пользу предпочтения одного действия другому в высшей степени убедительны | |
| 2,4,6,8 | Промежуточные значения между двумя соседними суждениями | Ситуация, когда необходимо компромиссное решение |
| Обратные величины приведенных выше ненулевых величин | Если действию i при сравнении с действием j приписывается одно из определенных выше ненулевых чисел, то действию j при сравнении с действием i приписывается обратное значение | Если согласованность была постулирована при получении N числовых значений для образования матрицы |
На основе этой шкалы ЛПР просят попарно сравнить объекты по какому-либо критерию. Результат парных сравнений заносятся в матрицу парных сравнений. Пример сравнения объектов по шкале представлен в табл. 5.4.
Таблица 5.4
Пример сравнения объектов по шкале
| № объекта | 1 | 2 | … | n |
| 1 | 1 | k1/k2 | … | k1/kn |
| 2 | k2/k1 | 1 | … | k2/kn |
| … | … | … | … | … |
| n | kn/k1 | kn/k2 | … | 1 |
где отношение ki/kj – выражает мнение эксперта о том, во сколько раз объект i лучше (хуже) объекта j.
Для получения конкретных оценок объектов по данному критерию существуют два основных подхода: первый – вычисление собственного вектора матрицы парных сравнений, второй – подсчет строчных сумм матрицы парных сравнений, а затем нормирование полученных значений. Сумма весовых коэффициентов подцелей или критериев одного уровня иерархии равна 1.
Также для получения оценок объектов могут использоваться метод Уэя и Коггера, которые будут описаны ниже.
Получение весовых коэффициентов критериев и подцелей происходит аналогично.
Оценка однородности суждений эксперта
При заполнении матриц парных сравнений экспертом могут быть допущены ошибки, которые нарушают количественную или транзитивную однородность суждений, так как человеческие суждения нельзя выразить точной формулой. Поэтому для улучшения однородности элементы, расположенные ниже главной диагонали, являются обратными величинами к соответствующим элементам, лежащим выше главной диагонали.
При нарушении однородности ранг матрицы парных сравнений отличен от единицы, и она будет иметь несколько собственных значений. При небольших отклонениях суждений от однородности одно из собственных значений будет существенно больше остальных и приблизительно равно порядку матрицы. Поэтому для оценки однородности суждений эксперта необходимо использовать отклонение величины максимального собственного значения λmax от порядка матрицы n [1, с. 35].
Однородность суждений оценивается индексом однородности ИО или отношением однородности ОО:
ИО=(λmax-n)/(n-1), (5.3)
ОО=ИО/М(ИО), (5.4)
где М(ИО) – среднее значение (математическое ожидание) индекса однородности случайным образом составленной матрицы парных сравнений [W], которое основано на экспериментальных данных (табл. 5.5) [1, с. 36].
Таблица 5.5
Среднее значение индекса однородности в зависимости от порядка матрицы
| Порядок матрицы n | М(ИО) | Порядок матрицы n | М(ИО) | Порядок матрицы n | М(ИО) |
| 0,00 | 1,24 | 1,51 | |||
| 0,00 | 1,32 | 1,48 | |||
| 0,58 | 1,41 | 1,56 | |||
| 0,90 | 1,45 | 1,57 | |||
| 1,12 | 1,49 | 1,59 |
В качестве допустимого значения используется значение ОО не более 0,1. Если для матрицы парных сравнений отношение однородности ОО больше 0,1, то это свидетельствует о существенном нарушении логичности суждений эксперта. Поэтому эксперту предлагается пересмотреть данные, использованные для построения матрицы.
Оценка однородности производится для всех матриц парных сравнений.
Расчет интегральных оценок объектов
Таким образом, на предыдущем шаге были получены весовые коэффициенты для всех элементов иерархии. Интегральная оценка объекта определяется как взвешенная сумма значений подцелей (критериев) второго уровня, которые в свою очередь вычисляются как взвешенные суммы значений критериев третьего уровня и так далее вплоть до получения значений критериев нижнего уровня иерархии.
Замечание. Для получения весовых коэффициентов критериев и подцелей иерархии могут быть привлечены несколько экспертов, каждый из которых заполняет матрицы парных сравнений. В этом случае в качестве весового коэффициента для элемента иерархии, соответствующего определенной вершине, рассматривается среднее геометрическое весовых коэффициентов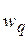 
, полученных по матрицам парных сравнений каждого из экспертов:
,
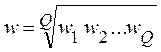где Q – количество экспертов.
Пример построения рейтинга компьютерных фирм на основе МАИ Саати
В качестве примера выбрана задача небольшой размерности с целью наглядно показать все этапы реализации метода.
1. Формирование иерархии (рис. 5.5).
Рис. 5.5. Иерархия для определения рейтинга фирмы
2. Получение оценок объектов, весовых коэффициентов критериев и подцелей.
Для получения весовых коэффициентов критериев эксперту предлагается оценить «важность» критериев по 9-бальной шкале. Результаты сравнения заносятся в табл. 5.6.
Таблица 5.6
Результаты сравнения критериев экспертом
| Название критерия | Качество обслуживания | Месторасположение |
| Качество обслуживания | 3/1 | |
| Месторасположение | 1/3 |
По шкале, предложенной Саати, значение «3/1» означает, что, по мнению эксперта, критерий «качество обслуживания» (КО) незначительно превосходит по значимости критерий «месторасположение фирмы» (МФ). Вычисление весовых коэффициентов важности критериев с помощью строчных сумм представлено в табл. 5.7.
Таблица 5.7
Вычисление весовых коэффициентов с помощью строчных сумм
| Критерий | КО | МФ | Строчная сумма | Нормированное значение весового коэффициента | Обозначение весового коэффициента |
| КО | 3/1 | 4/5.33=0.75 | w1 | ||
| МФ | 1/3 | 1.33 | 1.33/5.33=0.25 | w2 | |
| Сумма | 5.33 |
Значения критериев для фирм вычисляются аналогично. Результаты сравнений, а также значения критериев приведены в
табл. 5.8 и 5.9.
Таблица 5.8
Сравнение фирм по критерию «качество обслуживания»
| № фирмы | Строчная сумма | Нормированное значение критерия | Обозначение значения критерия | |||
| 7/1 | 3/1 | 0.59 | k11 | |||
| 1/7 | 1/5 | 1.34 | 0.07 | k12 | ||
| 1/3 | 5/1 | 6.33 | 0.34 | k13 | ||
| Сумма | 18.67 |
Таблица 5.9
Сравнение фирм по критерию «место расположения»
| № фирмы | Строчная сумма | Нормированное значение критерия | Обозначение значения критерия | |||
| 1/5 | 1/7 | 1.48 | 0.07 | k21 | ||
| 5/1 | 1/3 | 6.33 | 0.34 | k22 | ||
| 7/1 | 3/1 | 0.59 | k23 | |||
| Сумма | 18.81 |
Весовые коэффициенты важности критериев и значения критериев фирм также могут быть вычислены как собственные векторы матрицы парных сравнений.
3. Оценка однородности иерархии.
Для каждой из матриц парных сравнений вычислим индекс однородности и отношение однородности по формулам (5.3) и (5.4). Результаты представлены в табл. 5.10.
Таблица 5.10
Значения индекса однородности для матриц парных сравнений
| Матрица парных сравнений | Отношение однородности |
| весовых коэффициентов | 0.00 |
| фирм по критерию КО | 0.05 |
| фирм по критерию МФ | 0.05 |
4. Расчет интегральных оценок приведен в табл. 5.11.
Таблица 5.11
Расчет интегральных оценок
| № фирмы | Формула | Значение | Рейтинг фирмы |
| w1*k11+w2*k21 | 0.75*0.59+0.25*0.07=0.459 | ||
| w1*k12+w2*k22 | 0.75*0.07+0.25*0.34=0.138 | ||
| w1*k13+w2*k23 | 0.75*0.34+0.25*0.59=0.401 |
Дата добавления: 2015-05-28; просмотров: 1731;