Метод поиска медианы Кемени
Метод поиска медианы Кемени позволяет найти такое итоговое ранжирование P, суммарное расстояние от которого до всех заданных ранжирований минимальное:
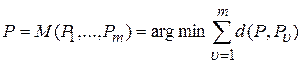 ,
,
где m – количество экспертов, P1, …, Pm – ранжирования, d(P,Pu) – расстояние между ранжированиями [5, с. 73].
Таким образом, для поиска медианы необходимо ввести понятие расстояния между ранжированиями. Оно определяется с помощью матриц отношений 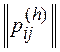 ,
, 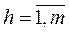 ,
, 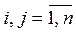 , n – количество альтернатив.
, n – количество альтернатив.

ri, rj – ранги i-той и j-той альтернатив в ранжировании h-ого эксперта. Отметим, что ранги альтернатив сравниваются наоборот, то есть ранг ri=1>rj=2 (ранг 1 больше ранга 2) и ri=5<rj=3 (ранг 5 меньше ранга 3).
Расстояние от произвольного ранжирования P, которому соответствует матрица 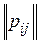 , до всех ранжирований P1, P2, …, Pm, которым соответствуют матрицы парных отношений
, до всех ранжирований P1, P2, …, Pm, которым соответствуют матрицы парных отношений 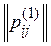 , …,
, …, 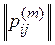 определяется по формуле:
определяется по формуле:
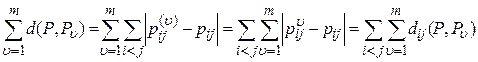 .
.
Для нахождения медианы Кемени вводится матрица потерь 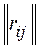 ,
, 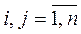 .
.
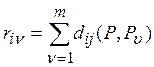 ,
,
где P – ранжирование, элемент матрицы отношений pij которого равен 1.
При этом задача поиска медианы Кемени для ранжирований формулируется как задача отыскания такого упорядочения альтернатив, а следовательно, строк и столбцов матрицы потерь, чтобы сумма ее элементов, расположенных над диагональю, была минимальна.
Эвристический алгоритм поиска медианы Кемени
Пусть для исходных ранжирований матрица потерь определена. Процесс поиска итогового ранжирования состоит из 2 этапов.
На первом этапе строится предварительное ранжирование PI.
1-я итерация. Подсчитаем суммы элементов строк матрицы потерь:
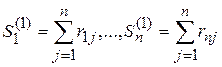 .
.
Найдем минимальную из них  .
.
Альтернативу аi1, ставим на первое место в искомом ранжировании. Вычеркивая в 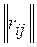 строку и столбец с номером i1, получаем матрицу
строку и столбец с номером i1, получаем матрицу 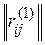 , множество индексов строк и столбцов которой соответственно I(1)=J(1)={1,…,n}\ I1.
, множество индексов строк и столбцов которой соответственно I(1)=J(1)={1,…,n}\ I1.
k-я итерация. В матрице потерь 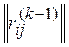 подсчитаем суммы элементов строк:
подсчитаем суммы элементов строк:
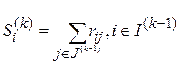 .
.
Найдем минимальную из них:
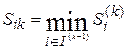 .
.
Альтернативу аik, ставим на k-тое место в искомом упорядочении. Вычеркивая в 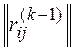 строку и столбец с номером ik, получаем матрицу
строку и столбец с номером ik, получаем матрицу 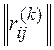 , множество индексов строк и столбцов которой соответственно I(k)=J(k)={1,…,n}\ {i1, …,ik}.
, множество индексов строк и столбцов которой соответственно I(k)=J(k)={1,…,n}\ {i1, …,ik}.
Алгоритм завершается после n-й итерации (I(k)=J(k) и равны пустому множеству). Искомое упорядочение

На втором этапе из найденного ранжирования PI получают итоговое ранжирование PII, при этом процесс перехода от ранжирования PI к ранжированию PII происходит следующим образом: для элементов ранжирования PI последовательно проверяем справедливость соотношений (1)
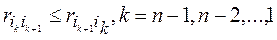 (6.1)
(6.1)
Как только для некоторого k оно нарушено, альтернативы aik и aik+1 в ранжировании меняем местами, а соотношение (6.1) проверяем, начиная с альтернативы, непосредственно предшествующей альтернативе, подвергшейся перестановке. После конечного числа шагов будет получено ранжирование PII.
Пример построения итогового ранжирования с помощью метода поиска медианы Кемени
Рассмотрим процесс построения итогового ранжирования на примере, рассмотренном ранее (исходные данные представлены в табл. 6.2).
1. Построим матрицы отношений для ранжирований экспертов:
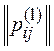
| 0 | -1 | -1 | -1 | 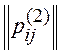
| 0 | -1 | -1 | -1 |
| 1 | 0 | -1 | 1 | 1 | 0 | 1 | 1 | ||
| 1 | 1 | 0 | 1 | 1 | -1 | 0 | 1 | ||
| 1 | -1 | -1 | 0 | 1 | -1 | -1 | 0 | ||
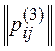
| 0 | 1 | 1 | 1 | 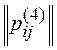
| 0 | 0 | -1 | -1 |
| -1 | 0 | -1 | -1 | 0 | 0 | -1 | -1 | ||
| -1 | 1 | 0 | 0 | 1 | 1 | 0 | -1 | ||
| -1 | 1 | 0 | 0 | 1 | 1 | 1 | 0 |
Например, p12(1)=-1, так как r1<r2 (r1=3, r2=1), p34(2)=0, так как r3=r4 (r3=2, r4=2).
2. Матрица потерь имеет следующий вид:
| 0 | 5 | 6 | 6 |
| 3 | 0 | 6 | 4 |
| 2 | 2 | 0 | 3 |
| 2 | 4 | 5 | 0 |
Например, r12=d12(P1,P3)+d12(P2,P3)+d12(P4,P3), так как P3 – ранжирование, элемент матрицы отношений которого p12(3)=1. Тогда r12=|p12(3)-p12(1)|+|p12(2)-p12(3)|+|p12(3)-p12(4)|=|1-(-1)|+ |1-(-1)|+ |1-0|=5.
3. Найдем предварительное ранжирование PI (первый этап).
1-я итерация. Подсчитаем
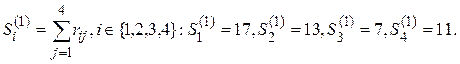
Минимум достигается на S3(1). На первое место в ранжировании PI помещается альтернатива a3, и она из дальнейших рассмотрений исключается.
2-я итерация. Подсчитаем 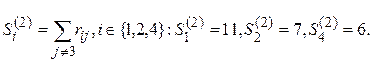
Минимум достигается на S4(2). На второе место в ранжировании PI помещается альтернатива a4, и она из дальнейших рассмотрений исключается.
3-я итерация. Подсчитаем 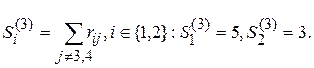
Минимум достигается на S2(3). На третье место в ранжировании PI помещается альтернатива a2, и она из дальнейших рассмотрений исключается. Таким образом, ранжирование PI имеет следующий вид:

4. Найдем ранжирование РII (второй этап).
Итак, i1=3, i2=4, i3=2, i4=1. Сравниваем 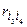 и
и 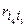 или r21 и r12, Так как r21≤r12 (3≤5), то альтернативы не меняем местами, переходим к сравнению r42 и r24. Так как r42≤r24 (4≤4), то переходим к сравнению r34 и r43. Поскольку r34<r43 (3≤5), то найденное ранжирование
или r21 и r12, Так как r21≤r12 (3≤5), то альтернативы не меняем местами, переходим к сравнению r42 и r24. Так как r42≤r24 (4≤4), то переходим к сравнению r34 и r43. Поскольку r34<r43 (3≤5), то найденное ранжирование

и является ранжированием РII, для которого соотношения (6.1) выполнены.
Итоговые ранжирования альтернатив по методу Борда и методу поиска медианы Кемени представлены в табл. 6.4.
Таблица 6.4
Результаты построения итогового ранжирования с помощью метода Борда и метода поиска медианы Кемени
| Альтернатива | Место в итоговом ранжировании (Кемени) | Место в итоговом ранжировании (Борд) |
| a1 | 4 | 3 |
| a2 | 2 | 4 |
| a3 | 1 | 1 |
| a4 | 3 | 2 |
Результаты работы описанных выше методов иногда могут различаться достаточно сильно. Метод Борда дает результаты, которые интуитивно понятны, так как в его основе лежит идея усреднения оценок. Что касается метода поиска медианы Кемени, то он, наоборот, может давать непредвиденные результаты. Для получения итогового ранжирования в методе используется специально оценка – расстояние между ранжированиями. А рассмотренный нами алгоритм получения итогового ранжирования основан на эвристике – предположении, что построенное таким образом итоговое ранжирование и будет наиболее близким к мнению всех экспертов с точки зрения введенной оценки.
Вопросы и задания
1. Приведите примеры групповых задач принятия решений.
2. Всегда ли можно найти лучшую альтернативу, используя правило большинства и принцип Кондорсе?
3. В чем принципиальные различие между методом Борда и методом поиска медианы Кемени?
Дата добавления: 2015-05-28; просмотров: 9031;
