Уравнение Клаузиуса - Клапейрона.

Процессы, заключающиеся в превращении одной фазы данного вещества в другую фазу того же вещества, т. е. протекающие без химических реакций называются фазовыми.

Примеры фазовых превращений (фазовых переходов) предложены в форме нижеследующих уравнений:

- испарение:

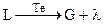, (4.73)

где - теплота испарения.

- сублимация (возгонка):

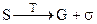, (4.74)

где 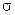- теплота сублимации.

- плавление:

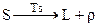, (4.75)

где - теплота плавления.

- полиморфное превращение:

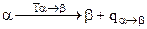, (4.76)

где - теплота полиморфного превращения. Например при Т = 910 ⁰С осуществляется полиморфное превращение, связанное с изменением типа кристаллической решетки железа: решетка 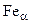типа О. Ц. К. перестраивается в решетку Г. Ц. К.

Основная характеристика фазового превращения - его температура, при которой фазы находятся в равновесии. Эта температура зависит от давления, например температура плавления льда или температура кипения воды изменяются с изменением величины давления.

Таким образом, состояние термодинамического равновесия двух фаз определяется соотношением между равновесной температурой и равновесным давлением.

Для установления этой связи рассмотрим две фазы (I и II) вещества, находящиеся в состоянии равновесия при р, Т = const. В этой ситуации справедливо равенство их молярных энергий Гиббса:

G_I = G_II. (4.77)

Условием сохранения равновесия при малых изменениях р и Т служит соотношение:

dG_I = dG_II. (4.78)

Согласно уравнению: dG = Vdp - SdT, (4.78) запишется в виде:

V_Idp - S_IdT = V_IIdp - S_IIdT, (4.78)

где V_I, V_II - молярные или удельные объемы фаз;

S_I, S_II - молярные или удельные энтропии фаз.

Из (4.78) следует:

(S_II - S_I)dT = (V_II - V_I)dp или 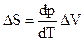, (4.79)

где .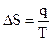

Тогда окончательно:

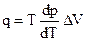, (4.80)

где q - энергетический эффект фазового перехода.

Полученное уравнение называется уравнением Клазиуса - Клапейрона и связывает термодинамические параметры (р и Т) между собой.

Для фазового перехода “испарение”, уравнение (4.80) приобретает форму:

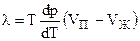, (4.81)

где V_П, V_Ж - молярные или удельные объемы пара и жидкости.

Так как > 0 и V_П >> V_Ж, то 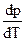> 0, т. е. с увеличением температуры, давление насыщенного пара увеличивается.

Так для воды = 2,25 МДж/кг, V_П = 1,65 м³/кг, V_Ж = 10^-3м³/кг, тогда 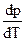= 3,61 кПа/К.

Для фазового перехода “сублимация”:

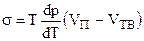, (4.82)

где V_ТВ - молярный или удельный объем твердой фазы.

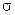> 0, V_П >> V_ТВ, поэтому 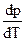> 0.

Для фазового перехода “плавление”:

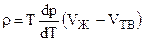, (4.83)

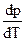> 0, обычно V_Ж > V_ТВ и > 0, т. е. с ростом давления в системе, температура фазового перехода увеличивается. Но для воды, Bi, Ga, некоторых марок чугунов V_Ж < V_ТВ и 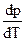< 0.

Так 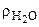= 334 кДж/кг; 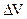= -0,09 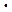10^-3 м³/кг и 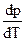= - 0,0753 К/МПа.

Для полиморфного превращения 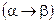уравнение Клазиуса - Клайперона (4.80) запишется:

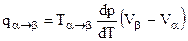. (4.84)

Если происходит превращение вида 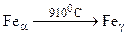, то = - 0,0082 К/МПа.

Рассматривая фазовый переход “испарение” можно получить частную форму записи уравнения (4.80).

Изменение объема в этом случае:

= V_П - V_Ж V_П.

Если пар - идеальный газ, то:

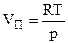, (4.85)

После замены:

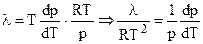или . (4.86)

Уравнение (4.86) - уравнение кривой давления насыщенного пара.

Точным его решением служит интеграл:

, (4.86)

где .

Тогда:

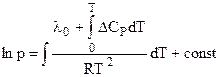или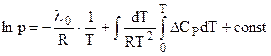

и окончательно:

, (4.87)

где 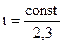- истинная химическая постоянная.

Таким образом, для нахождения величины давления насыщенного пара нужно знать 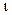и = f (Т).

Существуют и приближенные способы решения уравнения (4.87).

1. Пусть = const, т. е. = 0, тогда:

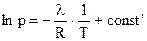. (4.88)

Это приближение слишком грубо и годится лишь для очень приближенной оценки величины давления.

2. Лучшим приближением является допущение, что = const, тогда .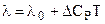

В этом случае:

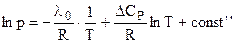. (4.89)

3. Следующее достаточно точное и часто применяемое приближение предложено Вальтером Нернстом: , тогда:

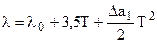. (4.90)

После решения уравнения (4.86) с учетом (4.90):

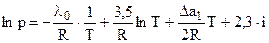, (4.91)

где i - условная химическая постоянная, причем .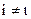

4. Более точный расчет может быть произведен с помощью таблиц термодинамических функций в стандартном состоянии, о чем будет сказано ниже.