Закон действующих масс и константа равновесия.
Химические реакции в обычных условиях их протекания принадлежат к числу необратимых процессов, идущих самопроизвольно лишь в одном направлении до тех пор, пока не будет достигнуто состояние термодинамического равновесия, называемое в данном случае химическим равновесием.
Одна из важнейших задач физической химии - определение этого состояния и выяснение влияния на него внешних условий.
Обычно говорят, что все химические реакции обратимы в том смысле, что в зависимости от условий они могут протекать как в прямом, так и в обратном направлении. Эта обратимость, впервые экспериментально доказанная Сен-Клер-Девилем (1857 г.) и Н. Н. Бекетовым (1862 г.) не идентична термодинамической обратимости и их не стоит смешивать.
Определение термодинамических параметров химического равновесия тесно связано с нахождением максимальной работы реакции. Наиболее наглядный и простой путь был дан Вант-Гоффом (1883 г.).
Для большей конкретизации можно начать с частного случая реакции между газами
3Н2 + N2 = 2NH3,
взятыми с произвольными начальными концентрациями продуктов реакции 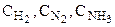 .
.
Необходимо заставить реакцию идти в изотермических условиях и обратимо в термодинамическом смысле. Это можно сделать с помощью “ящика Вант-Гоффа”, который представляет собой большой сосуд, наполненный смесью трех газов в произвольных количествах, достигнувшей состояния термодинамического равновесия 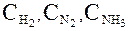 (рис. 4.5).
(рис. 4.5).
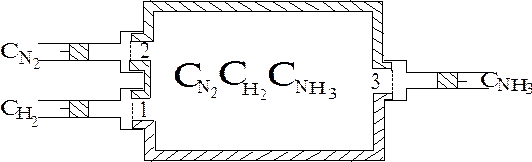
| Рис. 4.6. Ящик Вант-Гоффа. |
Ящик снабжен тремя окошками, затянутыми полупроницаемыми перегородками 1, 2 и 3, каждая из которых свободно пропускает только один из трех газов. Окошки снабжены заслонками. Газы при произвольных начальных концентрациях 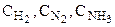 при Т = const находятся в трех больших резервуарах, каждый из которых тоже имеет окошко с заслонкой.
при Т = const находятся в трех больших резервуарах, каждый из которых тоже имеет окошко с заслонкой.
Рассматриваемый процесс состоит из трех следующих операций:
а) из резервуара с водородом при его концентрации 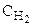 выводятся три моля водорода; их концентрация обратимо изменяется до
выводятся три моля водорода; их концентрация обратимо изменяется до 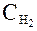 , после чего они вводятся через полупроницаемую перегородку 1 в равновесный ящик. При этом будет совершена работа:
, после чего они вводятся через полупроницаемую перегородку 1 в равновесный ящик. При этом будет совершена работа:
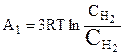 ;
;
б) та же операция одновременно проделывается с одним молем азота при переводе его из хранилища с концентрацией 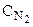 до
до 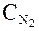 :
:
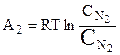 ;
;
в) те же операции, но в обратном порядке, одновременно проделываются с двумя молями аммиака, при переводе их из равновесного ящика с концентрацией 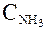 в резервуар с концентрацией
в резервуар с концентрацией 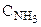 :
:
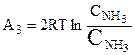 .
.
Поступая в равновесный сосуд, водород и азот реагируют с образованием аммиака. Выведение последнего из равновесного ящика с той же скоростью, с какой он образуется, не нарушает равновесия, а единственный результат всего процесса (кроме переноса энергии) будет превращение трех молей Н2 и одного моля N2 при их концентрациях 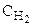 и
и 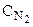 в два моля NH3 при концентрации
в два моля NH3 при концентрации 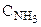 . Сумма всех работ равна максимальной работе реакции, т. к. все стадии процесса были проведены обратимо:
. Сумма всех работ равна максимальной работе реакции, т. к. все стадии процесса были проведены обратимо:
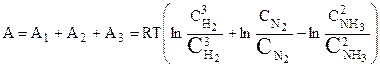
или
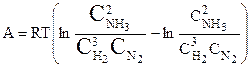 .
.
При изменении количества газов в равновесном ящике, состояние химического равновесия установится вновь, но с новыми равновесными концентрациями 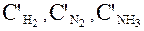 .
.
Повторение описанного выше процесса дает:
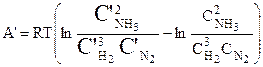 .
.
Так как оба процесса были совершены обратимо и изотермически с теми же начальными концентрациями, то А = А’ = AMAX или
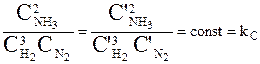 ,
,
где соотношение равновесных концентраций kC, называемое константой равновесия, есть для данной температуры величина постоянная, не зависящая от величин 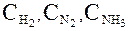 каждой в отдельности. Очевидно, что оно не зависит также от концентраций
каждой в отдельности. Очевидно, что оно не зависит также от концентраций 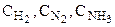 реагирующих газов, т. к. состояние смеси в равновесном ящике не связано с состоянием газов в резервуарах.
реагирующих газов, т. к. состояние смеси в равновесном ящике не связано с состоянием газов в резервуарах.
Выражение для kС, записанное выше - это математическая форма записи закона действующих масс: соотношение равновесных концентраций при Т = const есть величина постоянная и независящая от количеств реагирующих веществ.
Дата добавления: 2015-05-21; просмотров: 1242;
