Энергия Гиббса. Энергия Гельмгольца.

Энтропия - основная функция, позволяющая судить о направлении самопроизвольных процессов в изолированных системах. Чтобы использовать ее в практических целях нужно исследовать как самое систему, так и ее окружение. Хотя рассчитать изменение энтропии окружения или окружающей среды довольно просто 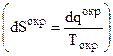, можно предложить метод, автоматически учитывающий наличие окружающей среды.

Из первого закона термодинамики следует:

dq = dU +dA.

Из второго закона:

dq 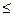TdS,

поэтому

TdS 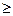dU + dA. (4.51)

Неревенство (4.51) представляет собой обобщенную форму записи первого и второго начал термодинамики.

Из (4.51) следует, что:

dA 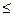TdS - dU. (4.52)

При постоянных Т и V (4.52) интегрируется непосредственно:

A_V 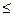T(S₂ - S₁) - (U₂ - U₁)

или

A_V 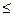TS₂ - TS₁ - U₂ + U₁,

откуда

A_V 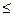-[( U₂ - TS₂) - (U₁ - TS₁)], (4.53)

где U - TS = F, поэтому:

A_V 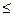-( F₂ - F₁) или 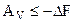. (4.54)

F - новая функция состояния, называемая энергией Гельмгольца (свободная энергия при постоянном объеме системы или изохорно-изотермический термодинамический потенциал).

Соотношение (4.54) читается: “... работа неизолированной системы в условиях V, T = const не более убыли энергии Гельмгольца”.

Величина А_Р = A_V - p 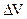есть величина максимальной полезной работы, где А_V - максимальная полная работа.

По аналогии А_Р может быть определена в виде разности двух значений некоторой функции G - энергии Гиббса:

A_Р 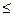-( G₂ - G₁) или . (4.55)

Так же как энтальпия отличается от внутренней энергии на величину pV, так и G отличается от F на величину pV:

G = F + pV = U - TS + pV = H - TS. (4.56)

Итак, окончательно:

F = U - TS и G = H - TS, (4.57)

где F и G - новые функции состояния.