ОБЕСПЕЧЕНИЕ ТРЕБУЕМОЙ ТОЧНОСТИ ИЗМЕРЕНИЙ
Многократное измерение одной и той же величины постоянного размера позволяет обеспечить требуемую точность.Поскольку ширина доверительного интервала зависит от количества экспериментальных данных, постольку, увеличивая и, можно добиться выполнения наперед заданного условия
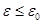
Упрощенный алгоритм обработки экспериментальных данных в этом случае показан на рис. 39.
Пример 18. В табл. 12 приведены 10 независимых числовых значении результата измерения линейного размера (в сантиметрах).
Таблица 12
| i | 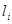
| 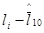
| 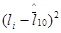
| i | 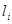
| 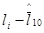
| 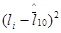
|
| -1 | -3 | ||||||
| -3 | |||||||
| -3 |
Определить его длину, если с вероятностью 0,95 точность измерения
должна быть не ниже 2 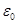 = 2 см.
= 2 см.
Решение. 1. Используя вспомогательные вычисления, сведенные в
табл. 12,получим
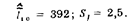
2. Больше чем на 3 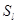 = 7,5 от среднего арифметического не отличается ни одно из числовых значении результата измерения. Таким образом, следует признать, что ошибок нет.
= 7,5 от среднего арифметического не отличается ни одно из числовых значении результата измерения. Таким образом, следует признать, что ошибок нет.
3. Допустим, есть основание полагать, что результат измерения подчиняется нормальному закону распределения вероятности
4. Стандартное отклонение среднего арифметического
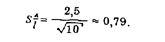
5. При п = 10 и Р = 0,95 по графику на рис. 38 находим t = 2,3.
6. Так как 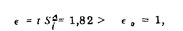
то необходимо увеличить количество экспериментальных данных (см. примечание на стр. 82).
7. Пусть 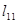 , = 390. Тогда
, = 390. Тогда
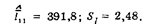
8. Для проверки нормальности закона распределения вероятности результата измерения используем составной критерий. При п = 11 и любой вероятности в табл. 11
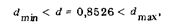
и ни одно из числовых значений 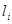 не отличается от 391,8 больше, чем на 2,5
не отличается от 391,8 больше, чем на 2,5 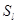 = 6,2. Таким образом, результаты проверки не противоречат гипотезе о том, что результат измерения подчиняется нормальному закону распределения вероятности.
= 6,2. Таким образом, результаты проверки не противоречат гипотезе о том, что результат измерения подчиняется нормальному закону распределения вероятности.
9. Стандартное отклонение среднего арифметического при n = 11
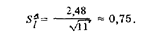
10. При п = 11 и Р = 0,95 t = 2,2.
Так как
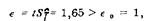
то необходимо еще больше увеличить количество экспериментальных данных.
11. Результаты последующих действий приведены в табл. 13.
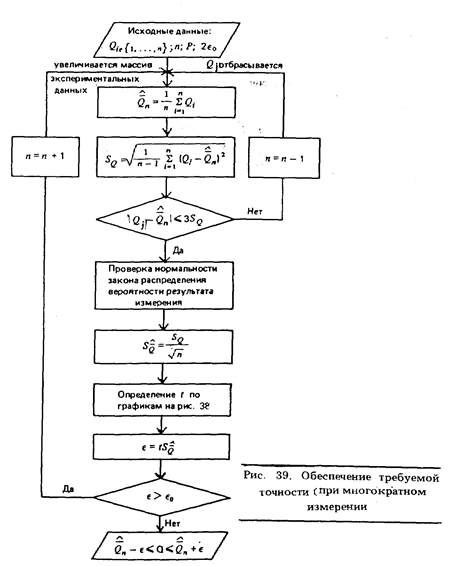
Таблица 13
| n | 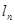
| 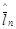
| 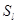
| 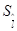
| t | 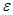
|
| 391,8 | 2,37 | 0,68 | 2,2 | 1,5 | ||
| 391,8 | 2,29 | 0,63 | 2 2 | 1.4 | ||
| 2,35 | 0,63 | 2.1'5 | 1,35 | |||
| IS | 391,9 | 2,28 | 0,59 | 2,15 | 1,27 | |
| 2.22 | 0,56 | 2,15 | 1,2 | |||
| 391,9 | 2,23 | 0?S4 | 2 1 | 1,13 | ||
| 2,16 | 0,51 | 2,1 | 1,07 | |||
| 2,15 | 0,49 | 2,1 | 1,04 | |||
| 2,14 | 0,48 | 2 1 | 1,01 | |||
| 2,13 | 0,47 | 2,1 | 0,98 |
Таким образом, потребовалось получить 21 числовое значение результата измерения для того, чтобы с вероятностью 0,95 установить, что1 == 391 . . . 393 см. Трудоемкость подобной работы требует автоматизации измерений и обработки экспериментальных данных.
На практике беспредельно повышать таким способом точность измерения не удается, так как рано или поздно определяющим становится не рассеяние отсчета и, следовательно, показания средства измерений, а недостаток информации (выражающийся, например, в незнании точного значения поправок и т.п.). Накапливать экспериментальные данные и уменьшать за счет этого стандартное отклонение среднего арифметического значения показания имеет смысл лишь до тех пор, пока по критерию (10) им нельзя пренебречь по сравнению с аналогом среднего квадратического отклонения, учитывающим дефицит информации (рис. 40). Точность многократного измерения, следовательно,ограничивается дефицитом информации.
Пример 19. При каком количестве экспериментальных данных в примере 14 можно получить максимально возможную точность измерения?
Решение.1. Для достижения максимальной точности количество экспериментальных данных нужно увеличивать до тех пор, когда по критерию (10) можно будет пренебречь sx по сравнению с uJ. Из условия
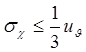
где sx = 2,0мм; uJ = 2,6мм, получим, что нужно sx уменьшить не менее, чем в 2,3 раза.
2. Накопление экспериментальных данных позволит перейти к среднему арифметическому значению показания. Для того, чтобы его стандартное отклонение
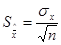
оказалось не менее, чем в 2,3 раза меньше sx, нужно получить п > 2,32 = 5 независимых отсчетов (не считая ошибок).
3. Для достижения еще большей точности нужно провести исследования, направленные на уточнение температурной поправки, и уменьшить uJ.
Дата добавления: 2015-02-05; просмотров: 1943;
