Сходящееся по вероятности к , при любом законе распределения вероятности результата измерения может служить состоятельной точечной оценкой среднего значения.
Математическое ожидание среднего арифметического
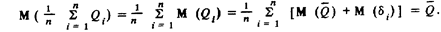
Поэтомусреднее арифметическое при любом законе распределениявероятности результатаизмерения является не толькосостоятельной, но и несмещенной оценкой среднегозначения. Этим обеспечивается правильность результата многократного измерения.
Точность результата многократного измерения зависит от эффективности оценки среднего значения. Чем она эффективнее (чем меньше ее рассеяние), тем выше точность (см. рис. 32). Критерии эффективности могут быть разными. При нормальном законе распределения вероятности наиболее популярным является такой показатель эффективности (мера рассеяния) , как сумма квадратов отклонений от среднего значения. Чем меньше этот показатель, тем эффективнее оценка. Это позволяет поставить задачу отыскания оценки среднего значения, наиболее эффективной по критерию

Такая задача называется задачей синтеза оптимальной (т.е. наилучшей в смысле выбранного критерия) оценки среднего значения, а метод ее решения, основанный на использовании критерия (12), —методом наименьших квадратов.
Исследуем функцию в левой части выражения (12) на экстремум. Она достигает минимума при
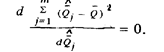
После возведения в квадрат и почленного дифференцирования получим
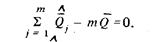
Если в качестве оценки 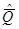 выбрать среднее арифметическое
выбрать среднее арифметическое 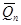 , то равенство
, то равенство
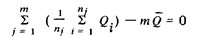
будет выполняться при п ®¥ в силу состоятельности этой оценки. Таким образом,среднее арифметическое является не только состоятельной и несмещенной, но и наиболее эффективной по критерию наименьших квадратов точечной оценкой среднего значения результата измерения.
В качестве точечной оценки дисперсии результата измерения по аналогии со средним арифметическим можно было бы взять
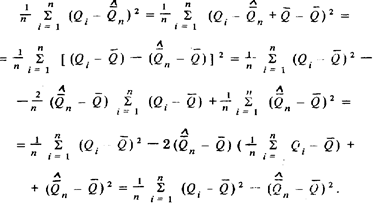
При любом законе распределения вероятности результата измерения эта оценка является состоятельной, так как при 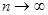 второе слагаемое в правой части стремится к нулю, а первое — к
второе слагаемое в правой части стремится к нулю, а первое — к 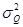 . Но
. Но
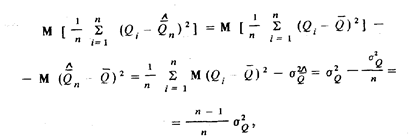
т.е. такая оценка является смещенной. Несмещенную оценку можно получить, умножив ее на коэффициент 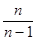
При 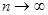 этот коэффициент стремится к 1, так что несмещенная точечная оценка дисперсии
этот коэффициент стремится к 1, так что несмещенная точечная оценка дисперсии
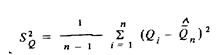
при любом законе распределения вероятности результата измерения остается состоятельной. Квадратный корень из нее
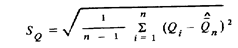
называется стандартным отклонением.
Оценив среднее значение Q и среднее квадратическое отклонение 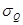 результата измерения, можно, используя вместо этих числовых характеристик точечные оценки
результата измерения, можно, используя вместо этих числовых характеристик точечные оценки 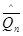 и
и 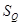 по правилу "трех сигм" проверить, не являются ли некоторые сомнительные значения
по правилу "трех сигм" проверить, не являются ли некоторые сомнительные значения 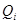 . ошибочными. Если окажется, что они отличаются от среднего арифметического
. ошибочными. Если окажется, что они отличаются от среднего арифметического 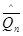 больше чем на 3
больше чем на 3 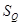 , то их следует отбросить (см. рис. 33). После этого рассчитываются окончательные значения
, то их следует отбросить (см. рис. 33). После этого рассчитываются окончательные значения 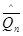 и
и 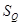 .
.
Пример 15. 15 независимых числовых значений результата измерения температуры в помещении по шкале Цельсия приведены во второй графе табл. 8
Таблица 8
| i | ti | ti- 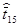
| (ti- 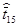 )2 )2
| ti- 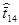
| (ti- 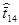 )2 )2
|
| 20,42 | + 0,016 | 0,000256 | + 0,009 | 0,000081 | |
| + 0,026 | +0,019 | ||||
| -0,004 | -0,011 | ||||
| + 0,026 | + 0,019 | ||||
| + 0,016 | + 0,009 | ||||
| + 0,026 | + 0,019 | ||||
| -0,014 | -0,021 | ||||
| -0,104 | - | - | |||
| -0,004 | -0,011 | ||||
| + 0,026 | + 0,019 | ||||
| + 0,016 | + 0,009 | ||||
| +0,006 | -0,001 | ||||
| -0,014 | -0,021 | ||||
| -0,014 | -0,021 | ||||
| -0,004 | -0,011 |
| i |
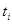
| 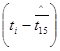
| 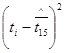
| 
| 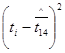
|
| 20,42 | + 0,016 | 0,000256 | + 0,009 | 0,000081 | |
| + 0,026 | +0,019 | ||||
| -0,004 | -0,011 | ||||
| + 0,026 | + 0,019 | ||||
| + 0,016 | + 0,009 | ||||
| + 0,026 | + 0,019 | ||||
| -0,014 | -0,021 | ||||
| -0,104 | |||||
| -0,004 | -0,011 | ||||
| + 0,026 | + 0,019 | ||||
| + 0,016 | + 0,009 | ||||
| +0,006 | -0,001 | ||||
| -0,014 | -0,021 | ||||
| -0,014 | -0,021 | ||||
| -0,004 | -0,011 |
Не допущено ли ошибок приих получении?
Решение. Среднее арифметическое результата измерения
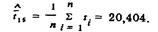
2. При определении стандартного отклонения результаты вспомогательных вычислений сведем в третью и четвертую графы табл. 8.
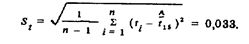
3. Большечем на 3 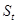 = 0,099 от среднего арифметического отличается восьмое значение. Следовательно, оно является ошибочным и должно быть отброшено.
= 0,099 от среднего арифметического отличается восьмое значение. Следовательно, оно является ошибочным и должно быть отброшено.
4. Без восьмого значения*
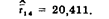
5. Результаты вспомогательных вычислений при повторном определении стандартного отклонения сведем в пятую и шестую графы табл. 8.
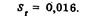
6. Ни одно из оставшихся значений 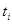 , не отличается теперь от среднего арифметического больше, чем на 3
, не отличается теперь от среднего арифметического больше, чем на 3 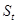 = 0,048. Можно, следовательно, считать, что среди них нет ошибочных.
= 0,048. Можно, следовательно, считать, что среди них нет ошибочных.
• При вычислении среднего арифметического часто приходится уменьшать или увеличивать число слагаемых. Для того чтобы не повторять всю процедуру суммирования и не перегружать память вычислительных устройств, удобно пользоваться формулой
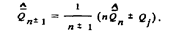
Универсальный метод отыскания эффективных оценок числовых характеристик любых законов распределения вероятности случайных чисел или величин разработан Р.А. Фишером. Он называется методом максимального правдоподобия. Сущность этого метода заключается в следующем.
Многомерная плотность распределения вероятности системы случайных значений р ( 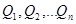 ) рассматривается как функция числовых характеристик закона распределения вероятности. Эта функция
) рассматривается как функция числовых характеристик закона распределения вероятности. Эта функция
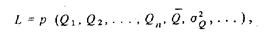
называемая функцией правдоподобия, показывает, насколько то или иное значение, каждой числовой характеристики "более правдоподобно", чем другие, функция правдоподобия достигает максимума при значениях переменных, являющихся их наиболее эффективными оценками. Последние, следовательно, находятся из условия
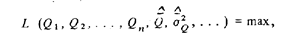
что равносильно совместному решению уравнений

Для упрощения вычислений функцию правдоподобия иногда логарифмируют, так как логарифм является монотонной функцией, то L и ln L достигают экстремума при одних и тех же значениях переменных. Наиболее эффективные оценки числовых характеристик, следовательно, могут определяться из совместного решения уравнений

Пример 16.Определить методом максимального правдоподобия эффективные оценки среднего значения и дисперсиии результата измерения, независимые равноточные значения которого подчиняются нормальному закону распределения вероятности.
Решение. 1, Плотность распределения вероятности каждого отдельного значения результата измерения
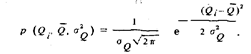
Поскольку все значения независимые, плотность распределения вероятности системы случайных величин
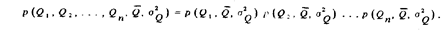
Таким образом функция правдоподобия
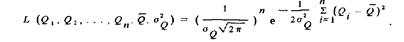
2. Логарифм функции правдоподобия
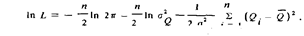
|
3. Уравнения, из которых находятся оценки:
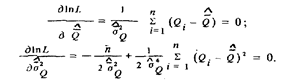
4. Решение первого уравнения
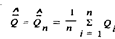
совпадает с результатом, полученным методом наименьших квадратов. 5. Решение второго уравнения

дает хотя и эффективную, но как мы видели, несколько смещенную оценку. К несмещенной оценке приводит введение поправочного множителя 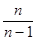
Дата добавления: 2015-02-05; просмотров: 1167;
