ОБРАБОТКА ЭКСПЕРИМЕНТАЛЬНЫХ ДАННЫХ, НЕ ПОДЧИНЯЮЩИХСЯ НОРМАЛЬНОМУ ЗАКОНУ РАСПРЕДЕЛЕНИЯ ВЕРОЯТНОСТИ

Если гипотеза о том, что результат измерения подчиня­ется нормальному закону распределения вероятности, отвер­гается, то существует несколько возможностей.

1. При особо точных и ответственных измерениях может быть поставлена задача определения закона распределения вероятности результата измерения. Однозначного решения она не имеет, и вывод о том, что экспериментально найден­ное распределение вероятности подчиняется какому-то кон­кретному закону, может быть сделан лишь с той или иной вероятностью. Основные требования к проведению иссле­дований, порядок математической обработки эмпирических данных и выбора математической модели распределения уста­новлены специальным документом Госстандарта МИ 199—79. Это довольно сложная и трудоемкая процедура, требующая значительных дополнительных затрат, и необходимость ее в каждом отдельном случае должна быть технико-экономичес-ки обоснована.

После определения с той или иной вероятностью вида за­кона распределения вероятности результата измерения, мето­дом максимального правдоподобия (см. разд. 2.6.1) уста­навливаются оценки его числовых характеристик и на осно­ве их использования разрабатывается вся последующая про­цедура обработки экспериментальных данных. Такая обработ­ка называется оптимальной и обеспечивает наивысшую точ­ность при выбранных критериях.

2. Если закон распределения вероятности результата изме­рения незначительно отличается от нормального (чаще всего это отличие проявляется в повышенной вероятности больших отклонений от среднего значения), то применяются так назы­ваемые робастные (устойчивые к отклонениям от нормального закона распределения вероятности) методы обработки экспе­риментальных данных. Все они основаны на ослаблении влия­ния больших отклонений от среднего значения на его оцен­ку.

В простейшем случае большие отклонения просто отбра­сываются, что приводит к усеченному нормальному закону распределения вероятности результата измерения (см. табл. 7). В этом случае оценкой среднего значения становится меди­ана закона распределения вероятности результата измерения

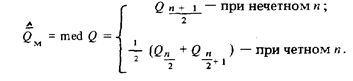
В некоторых случаях большие отклонения не отбрасыва­ются, а заменяются на ближайшие из оставшихся значений результата измерения, либо включаются в обработку с малы­ми весовыми коэффициентами. Порядок дальнейшей обработ­ки экспериментальных данных не меняется. Предельным слу­чаем усечения является оставление одного (при нечетном п) или двух (при четном л) значений результата измерения.

Среднее арифметическое не относится к устойчивым (робастным) оценкам. Объясняется это тем, что даже очень редкие большие отклонения (выбросы), не подчиняющие­ся нормальному закону распределения вероятности, играют по критерию (12) существенную роль. Операция возведения в квадрат делает их доминирующими среди слагаемых, а эффективность оценки, полученной методом наименьших квадратов, резко падает.

Ослабление влияния больших отклонений на оценку сред­него значения (т.е. повышение ее устойчивости) достигается при синтезе оценки по критерию эффективности, в котором квадратичная зависимость заменена на более слабую. Пока­зателем эффективности (мерой рассеяния), в частности, мо­жет бытьсумма отклонений от среднего значения или не­которая ее функция. Оценки, синтезированные по критерию

называются М-оценками. Функция 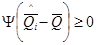при малых значениях аргумента выбирается близкой к квадратичной, а при больших — возрастающей медленнее, чем квадратичная. В зависимости от вида этой функции различают робастные оценки Хубера, Хампела, Андрюса, Тьюки и другие. Все они слабо зависят от выбросов и отклонений от нормального за­кона распределения вероятности, а в случае, когда результат измерения подчиняется нормальному закону, близки к оценке среднего значения, полученной методом наименьших квадра­тов.

Разновидностью М-оценок являются 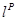- оценки, получаемые при

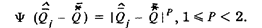
В отличие от перечисленных М-оценок они более эффективны вблизи других законов распределения вероятности, отличных от нормального. В частности, l¹ -оценка или оценка наимень­ших модулей, получаемая из условия

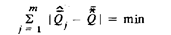
и совпадающая с медианой, оптимальна при экспоненциаль­ном законе распределения вероятности результата измерения.

Используются и другие робастные оценки.

3. С невысокой точностью значение измеряемой величины можно установить даже не интересуясь законом распределе­ния вероятности результата измерения. Среднее арифметичес­кое в этом случае может оказаться неэффективной оценкой, но его все равно целесообразно использовать, так как при всех обстоятельствах дисперсия среднего арифметического согласно соотношению (11) в п раз меньше дисперсии резуль­тата измерения, оценка которой на основании пятого свойства дисперсии (см. разд, 2.2) может быть представлена в виде

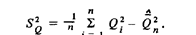
Стандартное отклонение среднего арифметического при лю­бом законе распределения вероятности

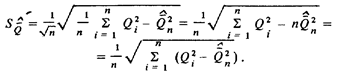
Задавшись доверительной вероятностью Р, по нижней кри­вой на рис. 22 можно определить, на сколько 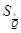среднее ариф­метическое 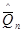может отличаться от среднего значения резуль­тата измерения 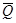при любом законе распределения вероят­ности. С неменьшей вероятностью

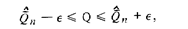
где, как обычно, - половина доверительного интер­вала.

Соответствующий порядок действий показан на рис. 33.