ОДНОКРАТНОЕ ИЗМЕРЕНИЕ
Подавляющее большинство измерений являются однократными. Можно сказать, что в обиходе, в торговле, во многих областях производственной деятельности выполняются только однократные измерения. В обычных условиях их точность вполне приемлема, а простота, высокая производительность (количество измерений в единицу времени) и низкая стоимость (по оценке трудозатрат) ставят их вне конкуренции. Многие люди до конца своей жизни остаются знакомыми только с однократными измерениями.
Результат однократного измерения описывается выражением (5), приведенным в разд. 2.1. Сам по себе он ни о чем еще не говорит, так как является случайным значением измеряемой величины. Необходимымусловием проведения однократного измерения служитналичие априорной информации. К ней относится, например, информация о виде закона распределения вероятности показания и мере его рассеяния, которая извлекается из опыта предшествующих измерений. Если ее нет, то используется информация о том, на сколько значение измеряемой величины может отличаться от результата однократного измерения. Такая информация бывает представлена классом точности средства измерений (см. разд. 4.1). К априорной относится информация о значении аддитивной или мультипликативной поправки (для конкретности ограничимся рассмотрением аддитивной поправки 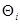 ). Если оно не известно, то это учитывается ситуационной моделью, согласно которой с одинаковой вероятностью, например, значение поправки может быть, любым в пределах от
). Если оно не известно, то это учитывается ситуационной моделью, согласно которой с одинаковой вероятностью, например, значение поправки может быть, любым в пределах от 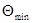 до
до 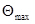 . Без априорной информации выполнение однократного измерения бессмысленно.
. Без априорной информации выполнение однократного измерения бессмысленно.
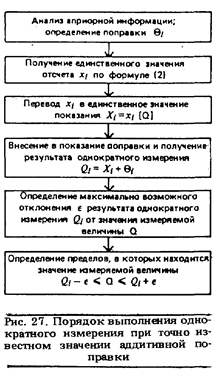
Порядок действий при однократном измерении показан на рис. 27. Предварительно проводится тщательный анализ априорной информации. В ходе этого анализа уясняется физическая сущность изучаемого явления, уточняется его модель, определяются влияющие факторы и меры, направленные на уменьшение их влияния (термостатирование, экранирование, компенсация электрических и магнитных полей и др.), значения поправок, принимается решение в пользу той или иной методики измерения, выбирается средство измерений, изучаются его метрологические характеристики и опыт выполнения подобных измерений в прошлом. Важном итогом .этой предварительной работы должна стать твердая уверенность в том, что точности однократного Измерения достаточно для решения поставленной задачи. Если это условие выполняется, то после необходимых приготовлений, включающих установку и подготовку к работе средства измерений, исключение или компенсацию влияющих факторов, выполняется основная измерительная процедура —получение одного значения отсчета.
|
Отсчет, согласно основному постулату метрологии, является случайным числом. Ни одно из отдельных его значений не дает полного представления о таком числе. Поэтому уже на этапе получения отсчета возникает дефицит измерительной информации, который может быть восполнен только за счет априорных сведений.
Единственное значение отсчета  дает одно единственное значение показания
дает одно единственное значение показания  средства измерений, имеющее ту же размерность, что и измеряемая величина. В это значение показания вносится поправка
средства измерений, имеющее ту же размерность, что и измеряемая величина. В это значение показания вносится поправка 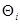 . Если ее значение известно точно, то результат измерения Q будет представлен единственным значением
. Если ее значение известно точно, то результат измерения Q будет представлен единственным значением
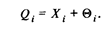
Если значение поправки не известно, то при выбранной ситуационной модели результат однократного измерения 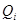 , с одинаковой вероятностью может быть любым в пределах от
, с одинаковой вероятностью может быть любым в пределах от  +
+ 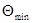 до
до  , +
, + 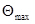 , ибо в последнем выражении
, ибо в последнем выражении 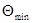
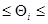
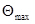 . Конечной целью измерительного эксперимента является получение достоверной количественной информации о значении измеряемой величины Q. На пути к достижению этой целиполучение результата однократного измерения служит промежуточным этапом. Дальнейшее зависит от того, какая используется априорная информация. Проанализируем несколько конкретных вариантов.
. Конечной целью измерительного эксперимента является получение достоверной количественной информации о значении измеряемой величины Q. На пути к достижению этой целиполучение результата однократного измерения служит промежуточным этапом. Дальнейшее зависит от того, какая используется априорная информация. Проанализируем несколько конкретных вариантов.
Вариант 1. Априорная информация: отсчет, а следовательно, и показание подчиняются нормальному закону распределения вероятности со средним квадратическим отклонением 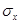 ; точное значение аддитивной поправки равно
; точное значение аддитивной поправки равно 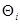 .
.
В этом случае результат измерения Q подчиняется нормальному закону распределения вероятности со средним квадратическим отклонением  =
= 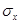 , но смещенному по отношению к закону распределения вероятности показания на значение поправки
, но смещенному по отношению к закону распределения вероятности показания на значение поправки 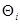 , внесение которой обеспечивает правильность измерения. Задавшись доверительной вероятностью Р, можно по верхней кривой на рис. 22 определить, на сколько
, внесение которой обеспечивает правильность измерения. Задавшись доверительной вероятностью Р, можно по верхней кривой на рис. 22 определить, на сколько  результат однократного измерения
результат однократного измерения 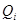 , может отличаться от среднего значения результата измерения
, может отличаться от среднего значения результата измерения 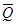 , равного значению измеряемой величины Q. Обозначив половину доверительного интервала через
, равного значению измеряемой величины Q. Обозначив половину доверительного интервала через 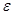 =t
=t  найдем, что с выбранной вероятностью
найдем, что с выбранной вероятностью
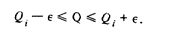
Вариант 2. Априорная информация: отсчет, а следовательно и показание подчиняются равномерному закону распределения вероятности с размахом 2 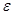 =
= 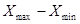 ; точное значение аддитивной поправки равно
; точное значение аддитивной поправки равно 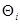 .
.
Такой вариант встречается при люфте подвижной части измерительного механизма. Результат измерения Q подчиняется равномерному закону распределения вероятности с тем же размахом , но смещенному по отношению к закону распределения вероятности показания на значение поправки 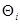 , внесением которой обеспечивается правильность измерения. Значение измеряемой величины Q, равное среднему значению результата измерения
, внесением которой обеспечивается правильность измерения. Значение измеряемой величины Q, равное среднему значению результата измерения 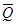 , находится в пределах
, находится в пределах
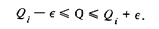
Вариант 3. Априорная информация: отсчет, а следовательно и показание подчиняются неизвестному закону распределения вероятности со средним квадратическим отклонением 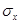 ; точное значение аддитивной поправки равно
; точное значение аддитивной поправки равно 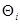 .
.
В данном случае закон распределения вероятности результата измерения неизвестен, известно лишь его среднее квадратическое отклонение  =
= 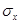 . Вероятность того, что результат однократного измерения
. Вероятность того, что результат однократного измерения 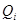 , окажется за пределами доверительного интервала при любом законе распределения вероятности
, окажется за пределами доверительного интервала при любом законе распределения вероятности
Введем в рассмотрение функцию 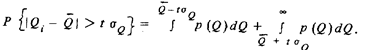
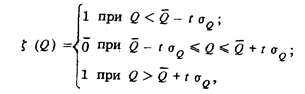
график которой показан на рис. 28. Это позволит перейти к более компактной записи:
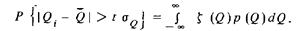
Результат интегрирования не уменьшится, если функцию 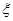 (Q) заменить показанной на рис. 28 пунктиром квадратичной функцией
(Q) заменить показанной на рис. 28 пунктиром квадратичной функцией  , которая при всех Q не меньше
, которая при всех Q не меньше 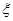 (Q).
(Q).
Тогда
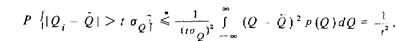
Вероятность того, что результат однократного измерения Q, при любом законе распределения вероятности не отличается от среднего значения больше, чем на половину доверительного интервала,
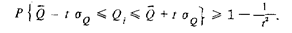
Полученная формула носит название неравенства П.Л. Чебышева. Она устанавливает нижнюю границу вероятности того что ни при каком законе распределения вероятности случайное' значение результата измерения не окажется за пределами доверительного интервала. Эта граница соответствует на рис. 22 нижней кривой.
При симметричных законах распределения вероятности результата измерения неравенство П.Л. Чебышева имеет вид
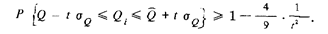
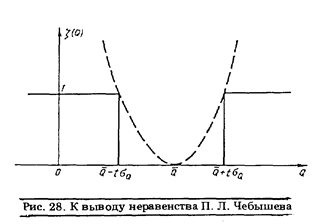
Соответствующая граница проходит выше и левее. На рис. 22 она показана пунктиром.
Задавшись доверительной вероятностью Р, можно по нижней кривой на рис. 22 определить, на сколько  результат однократного измерения
результат однократного измерения 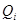 может отличаться от среднего значения результата измерения
может отличаться от среднего значения результата измерения 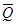 , равного значению измеряемой величины Q, при любом законе распределения вероятности. Обозначив, как и ранее, половину доверительного интервала через
, равного значению измеряемой величины Q, при любом законе распределения вероятности. Обозначив, как и ранее, половину доверительного интервала через 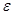 =t
=t  , найдем, что с неменьшей вероятностью
, найдем, что с неменьшей вероятностью
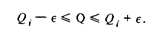
Вариант 4. Априорная информация: класс точности средства измерений таков, что значение измеряемой величины не может отличаться от результата однократного измерения больше, чем на 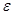 ; точное значение аддитивной поправки равно
; точное значение аддитивной поправки равно 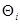 .
.
Этот вариант ничем не отличается от второго. Значение измеряемой величины
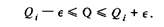
Вариант 5. Априорная информация: отсчет, а следовательно, и показание подчиняются нормальному закону распределения вероятности со средним квадратическим отклонением 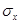 ; значение аддитивной поправки находится в пределах от
; значение аддитивной поправки находится в пределах от 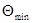 до
до 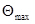 .
.
Ситуационной моделью, учитывающей неопределенность значения поправки, является равномерный закон распределения вероятности 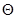 на интервале от
на интервале от 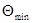 до
до 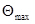 . Закон распределения вероятности результата измерения Q представляет собой композицию законов распределения вероятности показания и ситуационной модели. Композиция, в которую входит ситуационная модель, не подчиняется вероятностно-статистическим закономерностям. Однако по аналогии с вариантом 1 в 1981 году Международный комитет мер и весов рекомендовал считать, что с высокой вероятностью среднее значение композиции, равное значению измеряемой величины, не отличается от результата однократного измерения больше,
. Закон распределения вероятности результата измерения Q представляет собой композицию законов распределения вероятности показания и ситуационной модели. Композиция, в которую входит ситуационная модель, не подчиняется вероятностно-статистическим закономерностям. Однако по аналогии с вариантом 1 в 1981 году Международный комитет мер и весов рекомендовал считать, что с высокой вероятностью среднее значение композиции, равное значению измеряемой величины, не отличается от результата однократного измерения больше,
чем на 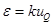 , где
, где 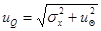 , а коэффициент k, аналогичный .коэффициенту k, устанавливается по соглашению. Обычно он принимается равным 2 ... 3.
, а коэффициент k, аналогичный .коэффициенту k, устанавливается по соглашению. Обычно он принимается равным 2 ... 3.
Пример 14. Единственное значение отсчета в условиях, рассмотренных в примере 12, равно 1. Из опыта предшествовавших измерений известно, что отсчет подчиняется нормальному закону распределения вероятности со средним квадратическим отклонением 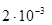 . В каких пределах находится значение измеренного линейного размера?
. В каких пределах находится значение измеренного линейного размера?
Решение 1. Единственное значение показания равно 1 м. Показание подчиняется нормальному закону распределения вероятности со средним квадратическим отклонением 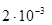 м.
м.
2. Ситуационная модель, учитывающая дефицит информации о значении аддитивной температурной поправки, представлена графически на рис. 18, б. Ее числовые характеристики 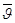 = 5,5 мм;
= 5,5 мм; 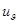 = 2,6мм.
= 2,6мм.
3. Аналог среднего квадратического отклонения результата измерения

4. Принимая k = 2, и выбирая в качестве результата однократного измерения 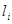 = 1000 + 5,5 = 1005,5 мм, получим
= 1000 + 5,5 = 1005,5 мм, получим
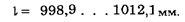
Рассмотренный пример позволяет сделать несколько замечаний.
Замечание 1.Получение результата измерения служит промежуточным этапом, на котором измерительная информация должна представляться в форме, удобной для ее дальнейшей обработки (переработки). Такой формой является представление результата измерения с помощью числовых характеристик закона распределения вероятности. При однократном измерении чаще всего используется такая числовая характеристика закона распределения вероятности, как среднее квадратическое отклонение (или его аналог). С ее помощью определяются пределы, в которых находится значение измеряемой величины, осуществляется внесение поправки, точное значение которой неизвестно. Если пользоваться стандартными аппроксимациями законов распределения вероятности, представленными в табл. 7, то переход к этой числовой характеристике удобно осуществлять с помощью коэффициентов, приведенных в третьей графе.
Замечание 2. Цель измерения состоит в уточнении значения измеряемой величины. Если измерительная информация не предназначена для дальнейшей обработки (переработки) , то она должна быть представлена в форме, удобной для восприятия человеком. Такой формой является указание пределов, в которых находится значение измеренной величины. Не рекомендуется пользоваться записью Q =  ,так как в силу особенностей человеческой психики при этом возникает некоторая доминанта, акцент на середину интервала, для чего нет никаких оснований. Все значения Q в интервале
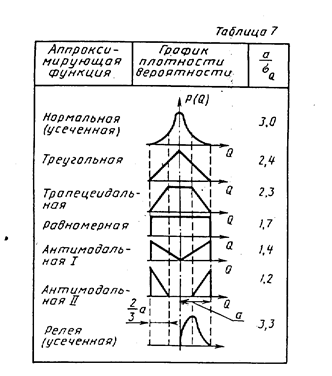
,так как в силу особенностей человеческой психики при этом возникает некоторая доминанта, акцент на середину интервала, для чего нет никаких оснований. Все значения Q в интервале 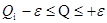 Q, равноправны.
Q, равноправны.
Замечание 3. Внесение поправки, точное значение которой неизвестно, с одной стороны смещает интервал, в пределах которого находится значение измеряемой величины,
а с другой — расширяет его. Из рассмотрения рис. 29 следует, что внесение неточно известной поправки целесообразно только тогда, когда
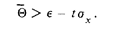
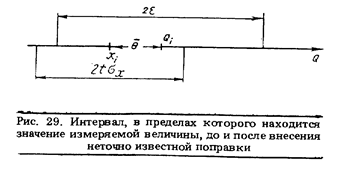
Замечание 4 касается достоверности измерений. Под достоверностью понимается степень доверия к тому, что значение измеренной величины находится в указанном интервале. Рассмотрим два случая, чаще всего встречающиеся на практике.
1. Результат измерения подчиняется нормальному закону распределения вероятности (см., например, вариант 1), что бывает чаще всего при точно известном значении поправки. Точность результата измерения (см. рис. 30) в этом случае равна точности показания, которая в свою очередь характеризует точность средства измерений. Ширина интервала, в котором устанавливается значение изменяемой величины, зависит от выбранной доверительной вероятности. Чем выше эта вероятность, тем с большей гарантией, с большей достоверностью устанавливается значение измеряемой величины. С вероятностью 0,95
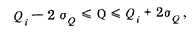
с вероятностью 0,99
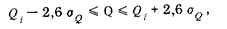
с вероятностью 0,997
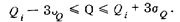
Такимобразом, в рассматриваемом случаедоверительная вероятность является мерой достоверности измерений.
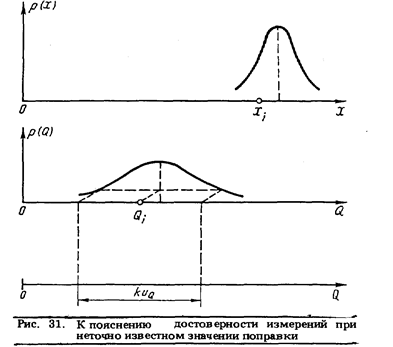
2. Результат измерения описывается композицией закона распределения вероятности показания и ситуационной модели, учитывающей неточность значения поправки (рис. 31). Достоверность измерений в этом случае обеспечивается выбором коэффициента k.
Замечание 5 связано с правилами округления. В метрологии принято среднее квадратическое отклонение или его аналог выражать одной значащей цифрой, например, 8; 0,5; 0,007. Две значащие цифры, например, 27; 0,016 удерживаются при особо точных измерениях и в тех случаях, когда значащая цифра старшего разряда меньше 4 (в промежуточных вычислениях сохраняется на одну значащую цифру больше). Вследствие этого, при квадратичном суммировании
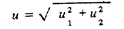
любым из слагаемых  , под радикалом можно пренебречь, еслиего учет почти не меняет и. Строго говоря, и при этом мо933
, под радикалом можно пренебречь, еслиего учет почти не меняет и. Строго говоря, и при этом мо933
цифрами то условие можно считать выполненным, если и - 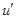 < 0,05 и, откуда 0,95 и <
< 0,05 и, откуда 0,95 и < 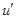 . Возводя обе части неравенства в квадрат и принимая во внимание, что (и' )2 =
. Возводя обе части неравенства в квадрат и принимая во внимание, что (и' )2 = 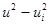 получим
получим
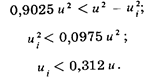
Таким образом.слагаемым
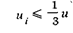
всегда можно пренебречь. Это правило распространяется и на сумму нескольких слагаемых.

жет уменьшиться до 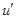 , но так как значение и выражается не более, чем двумя значащими
, но так как значение и выражается не более, чем двумя значащими
В п 2 3.4 отмечалось, что при измерениях никто не застрахован от ошибок. Может оказаться ошибочным и единственное значение отсчета  при однократном измерении. Во избежание такой ошибки однократное измерение рекомендуется 2…3 раза повторить без совместной обработки полученных
при однократном измерении. Во избежание такой ошибки однократное измерение рекомендуется 2…3 раза повторить без совместной обработки полученных
результатов.
2.6. МНОГОКРАТНОЕ ИЗМЕРЕНИЕ С РАВНОТОЧНЫМИ ЗНАЧЕНИЯМИ ОТСЧЕТА
Многократное измерение одной и той же величины постоянного размера производится при повышенных требованиях к точности измерений. Такие измерения характерны для профессиональной метрологической деятельности и выполняются в основном сотрудниками государственной и ведомственных метрологических служб, а также при тонких научных экспериментах. Это сложные, трудоемкие и дорогостоящие измерения, целесообразность которых должна быть всегда убедительно обоснована. Один из создателей теорий информации Л. Бриллюэн в статье “Теория информации и ее приложение к фундаментальным проблемам физики” привел слова Д. Габора о том, что "ничто не дается даром, в том числе информация". В полной мере это относится и к измерительной информации.
Результат многократного измерения описывается выражением (6)приведенным в разд. 2.1. Как и результат однократного измерения он является случайным значением измеряемой
величины, но его дисперсия
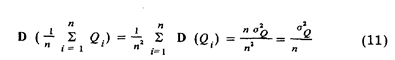
в п раз меньше дисперсии результата измерения Q. Благодаря такому обстоятельству, как это видно, например, на рис. 32, где выделены интервалы, соответствующие доверительной вероятности 0,95, точность определения значения измеряемой величины повышается в 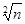 раз.
раз.
|
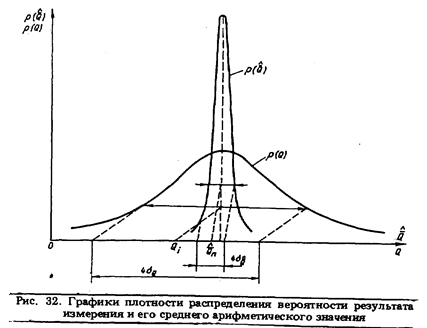
На рис. 32 показан случай, когда результат многократного измерения - среднее арифметическое значение результата измерения 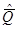 — подчиняется нормальному закону распределения вероятности. Так бывает всегда, когда нормальному закону распределения вероятности подчиняется сам результат измерения Q. Наличие массива экспериментальных данных
— подчиняется нормальному закону распределения вероятности. Так бывает всегда, когда нормальному закону распределения вероятности подчиняется сам результат измерения Q. Наличие массива экспериментальных данных
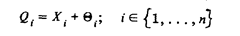
позволяет получить апостериорную информацию о законе распределения вероятности результата измерения. В частности, может быть поставлена задача его определения. Но чаще ограничиваютсяпроверкой нормальности закона распределения вероятности результата измерения и жертвуют точностью при отрицательных результатах проверки.
Другой возможностью, которая открывается благодаря наличию большого объема экспериментальных данных, является обнаружение и исключение ошибок по правилу "трех сигм". Таким образомспецифическая особенность многократного измерения состоит в эффективном использовании апостериорной измерительной информации.
Последнее вовсе не означает, что необходимость в анализе априорной информации отпадает. Такой анализ обязательно предшествует многократному измерению и преследует те же цели, что и при однократном измерении, но с той разницей, что при многократном измерении информация о законе распределения вероятности результата измерения получается опытным путем.
Вслед за анализом априорной информации и тщательной подготовкой к многократному измерению получают п независимых значений отсчета. Эта основная измерительная процедура может быть организована по-разному. Если изменением измеряемой величины по времени можно пренебречь, то все значения отсчета проще всего получить путем многократного повторения операции сравнения (2) с помощью одного и того же средства измерений. Отсчет в этом случае будет описываться эмпирической плотностью распределения вероятности р ( 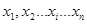 )- см. пример 4, где согласно основному постулату метрологии каждое значение отсчета является случайным числом, подчиняющимся этому закону распределения вероятности. Такие значения отсчета, имеющие одинаковую дисперсию, называются равноточными. Если же из априорной информации следует, что за время измерения произойдет существенное изменение измеряемой величины, то ее измеряют одновременно несколькими средствами измерений, каждое из которых дает одно из независимых значений отсчета xi. Так как средства измерений могут отличаться по точности, то в эмпирической плотности распределения вероятности отсчета p (
)- см. пример 4, где согласно основному постулату метрологии каждое значение отсчета является случайным числом, подчиняющимся этому закону распределения вероятности. Такие значения отсчета, имеющие одинаковую дисперсию, называются равноточными. Если же из априорной информации следует, что за время измерения произойдет существенное изменение измеряемой величины, то ее измеряют одновременно несколькими средствами измерений, каждое из которых дает одно из независимых значений отсчета xi. Так как средства измерений могут отличаться по точности, то в эмпирической плотности распределения вероятности отсчета p ( 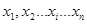 )- случайные числа
)- случайные числа  могут иметь разную дисперсию. Такие значения отсчета
могут иметь разную дисперсию. Такие значения отсчета  , называются неравноточными. Многократное измерение с неравноточными значениями отсчета рассматривается в следующем разделе.
, называются неравноточными. Многократное измерение с неравноточными значениями отсчета рассматривается в следующем разделе.
Порядок выполнения многократного измерения с равноточными значениями отсчета показан на рис. 33.
Всезначения отсчета  , независимо от способа их получения,переводятся в показания
, независимо от способа их получения,переводятся в показания  , в которыевносятся поправки
, в которыевносятся поправки 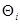 . Если многократное измерение выполняется одним средством измерений, то поправки могут отличаться друг
. Если многократное измерение выполняется одним средством измерений, то поправки могут отличаться друг
от друга из-за изменения во времени влияющих факторов, Если же используются одновременно несколько средств измерений, то поправки отличаются из-за индивидуальных особенностей каждого из них. Для простоты будем считать их известными точно.
Полученный массив экспериментальных данных может содержать ошибки. Причины появления ошибок и "правило. трех сигм", которым пользуются для их выявления, рассмотрены в разд. 2.3.4. Для того, чтобы воспользоваться этим правилом, нужно знать числовые характеристики закона распределения вероятности результата измерения — среднее значение 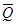 и среднее квадратическое отклонение
и среднее квадратическое отклонение  . Однако, как уже отмечалось в разд. 2.2, 2.4, вычислить их невозможно из-за конечного п и практической нереализуемости интегрирования в бесконечных пределах. Можно лишь как-то оценить эти числовые характеристики на основе ограниченного экспериментального материала, указать их приближенные значения или пределы, в которых они находятся с определенной вероятностью.
. Однако, как уже отмечалось в разд. 2.2, 2.4, вычислить их невозможно из-за конечного п и практической нереализуемости интегрирования в бесконечных пределах. Можно лишь как-то оценить эти числовые характеристики на основе ограниченного экспериментального материала, указать их приближенные значения или пределы, в которых они находятся с определенной вероятностью.
Рис. 33. Порядок выполнения многократного измерения при равноточных значениях отсчета 

2.6.1. ТОЧЕЧНЫЕ ОЦЕНКИ ЧИСЛОВЫХ ХАРАКТЕРИСТИК
Оценки числовых характеристик законов распределения вероятности случайных чисел или величин, изображаемые точкой на числовой оси, называются точечными. В отличие от самих числовых характеристик оценки являются случайными, причем их значения зависят от объема экспериментальных данных, а законы распределения вероятности — от законов распределения вероятности самих случайных чисел или значений измеряемых величин. Оценки должны удовлетворять трем требованиям: быть состоятельными, несмещенными и эффективными. Состоятельной называется оценка, которая сходится по вероятности к оцениваемой числовой характеристике. Несмещенной является оценка, математическое ожидание которой равно оцениваемой числовой характеристике. Наиболее эффективной считают ту из нескольких возможных несмещенных оценок, которая имеет наименьшее рассеяние.
Рассмотрим п независимых значений 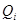 , полученных при измерении физической величины постоянного размера. Пусть, как и раньше (см. разд. 2.4), каждое из них отличается от среднего значения на случайное отклонение
, полученных при измерении физической величины постоянного размера. Пусть, как и раньше (см. разд. 2.4), каждое из них отличается от среднего значения на случайное отклонение 
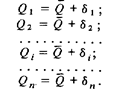
Сложив между собой левые и правые части этих уравнений и разделив их на n, получим:
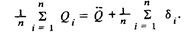
В пределе при п 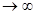
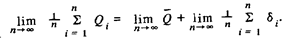
Здесь
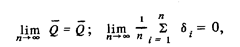
так чтосреднее арифметическое значение результата измерения
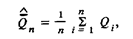
Дата добавления: 2015-02-05; просмотров: 2955;
