Расчеты колебательных спектров нанокристаллов

В настоящее время существуют технические возможности рассчитать колебательный спектр системы с достаточно большим числом атомов. Такие расчеты демонстрируют удовлетворительное согласие с экспериментом. Обычно используется геометрическая модель нанокристалла как идеального кристалла с конкретной структурой (например, для кристаллов группы A₂B₆ сфалерита или вюрцита), включающая определенное число элементарных ячеек кристалла. Краевые атомы в такой модели предполагаются свободными, а спектр нанокристалла рассматривается как спектр свободой квазимолекулы. В современных вычислительных программах модель включает кулоновское взаимодействие жестких заряженных ионов и близкодействующее отталкивание, описывающееся в приближении Борна-Кармана. Силовые константы, использующиеся при расчетах, должны давать экспериментальные частоты объемного кристалла.

В настоящее время в литературе рассчитаны колебательные спектры нанокристалла в форме кубиков различного размера, начиная с объекта, состоящего из одной ячейки – 111 (числа показывают количество ячеек в направлениях Х, Y, Z) и заканчивая объектом размера 555. (см. рис. 37).

а) б)

Рис. 37. Модели нанокристалла размером (в постоянных элементарной ячейки вдоль направлений x, y, z) – 111(а), 122(б).

На рис. 38 представлен спектр плотности колебательных состояний как объемного кристалла CdS, так и нанокристаллов в форме кубиков с размерами 2×2×2 и 5×5×5 (числа показывают количество элементарных ячеек в направлениях x, y, z). Результаты проведенных расчетов показывают, что уже при размерах нанообразований 8 – 10 элементарных ячеек наблюдается четкое разделение мод на акустические и оптические колебания, а в нанокристалле размера более 2×2×2 уже существует запрещенная зона частот в интервале 140 – 220 см^–1. При увеличении количества элементарных ячеек плотность распределения частот квантовой точки приближается к плотности распределения частот объемного кристалла.

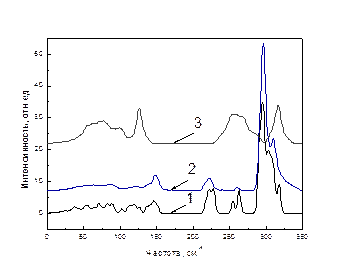
Рис. 38. Плотность распределения колебательных частот нанокристаллов разных размеров. Размер кристалла в количестве элементарных ячеек: 1 – (222); 2 – (555); 3 – объемный кристалл.

Рис. 39. Рассчитанные спектры КР нанокристаллов размера (2×2×2) в различных моделях: 1 – модель деформационного потенциала, 2 – модель фрелиховского взаимодействия.3 – экспериментальный спектр КР нанокристалла CdS.

На рис. 39 представлены вычисленный спектр рамановского рассеяния в приближении модели поляризуемости связей, а также спектр, сотоящий из линий, интенсивность которых пропорциональна квадрату дипольного момента каждой моды. Первый соответствует спектру рассеяния в модели деформационного потенциала, в то время как второй соответствует механизму фрелиховского взаимодействия. Для сравнения на рисунке показан экспериментальный спектр КР нанокристалла CdS.

Литература:

1. M.Cardona, P.Yu. Fundamentals of semiconductors. Springer, 1999.

2. Милехин А.Г.,Спектроскопия колебательных состояний низкоразмерных многослойных структур. Институт физики полупроводников СО РАН. Новосибирск, 2006

3. Zakhleniuk at all. Optical phonons confinement in nitride-based heterostructures. In III-Y Nitride Semiconductors. Ed. M.O.Manasreh, Elsevier, 2000.

4. S.M.Rytov, Zh.Eksp.Teor.Phys. 29, 605 (1955). [JETP, 2, 466 (1956)]