Квантованные полярные оптические моды

Принципиально другие возбуждения могут возникать в кристаллах, где существуют полярные моды. О существовании мод, обладающих дипольным моментом, хорошо известно. Многие моды в рассматриваемых полупроводниках являются полярными. Здесь мы обсудим явления, возникающие около интерфейсов (гетеропереходов) между двумя полупроводниками, из которых по крайней мере один является полярным. Сначала рассмотрим случай одиночного плоского гетероперехода, потом двойного гетероперехода (т.е. квантовой ямы) и, наконец, периодический случай сверхрешетки.

При рассмотрении фононов в таких двумерных структурах мы будем пренебрегать так называемыми эффектами запаздывания (т.е. поляритоном). Это означает, что длины волн рассматриваемых возбуждений предполагаются малыми по сравнению с длинами волн фотонов той же частоты, и следовательно, можно пренебречь волновой природой электрических полей, сопровождающих движение ионов. Эти поля имеют электростатическое происхождение, т.е. подчиняются только уравнению Гаусса и соответствующему уравнению Максвелла,

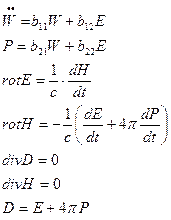. (11)

В этих уравнениях чтобы пренебречь эффектами запаздывания необходимо положить равной нулю производную по времени:

ÑE=0 divE =0 . (12).

В уравнении (12) подразумевается, что поле Еможно найти из скалярного потенциала ф{r), который должен удовлетворять уравнению Лапласа:

Ñ ²ф(r)=0,(13)

а также обычным граничным условиям непрерывности для компонент электрического смещения D_┴= ε_AE_┴перпендикулярного к интерфейсу, и непрерывности параллельных компонент поля E_||. Для одиночного интерфейса между двумя полупроводниками А и В с изотропными диэлектрическими функциями ε_A(ω)и ε_B(ω) должно выполняться:

E_||А = E_||В (14 а)

ε_AE_┴A= ε_AE_┴A (14 б)

Решения уравнения (13) при учете электростатических граничных условий (14),и того факта, что Е= –Ñф{r), можно представить в следующем виде. Мы предполагаем, что интерфейсом является плоскость z = 0, a z < 0 соответствует среде А.

Ф_A = Ae^iqxe^+qz при z < 0, (15а)

Ф_B = Be^iqx e^–qz при z >0, (15б)

где ось х выбрана вдоль направления вектора q, лежащего в плоскости, a q_z² = q_x², как следует из (13). Отметим, что (15) отражает наличие трансляционной симметрии (т.е. тот факт, что потенциалы ф должны быть функциями Блоха) вдоль х и у и отсутствие ее вдоль z. Потенциалы ф_а и ф_B сконцентрированы вблизи интерфейса, поскольку они экспоненциально затухают по мере удаления от z = 0. Моды, которые описываются такими функциями, называются интерфейсными модами.

Применение граничного условия (14а) к (15) приводит к равенству коэффициентов А = В,в то время как (14б) приводит к «секулярному уравнению» для частот интерфейсных мод ω_IF:

ε_A (ω_IF)= –ε_B (ω_IF) . (16)

Оно имеет решения только в том случае, когда существуют частоты, для которых две диэлектрические функции ε_A и ε_B имеют противоположные знаки.

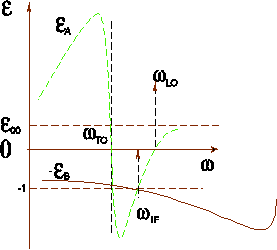
Рис. 19. Схема, иллюстрирующая получение решения для интерфейсного фонона ω _if из

(16) в случае контакта между полярным полупроводником А и неполярным В путем

построения зависимости ε_A и –ε_B от ω.

Следовательно, в случае интерфейса между полярным полупроводником (например, GaAs) и неполярным (например, Ge или Si) должна существовать одна интерфейсная мода в области частот ω_TO < ω _if < ω_lo (рис. 19), тогда как в случае интерфейса между двумя полярными полупроводниками, к примеру, GaAs и AlAs, должно быть две интерфейсных моды, одна GaAs-подобная, а другая AlAs-подобная.

Рассмотрим теперь случай квантовой ямы из материала В с барьером из материала А (см. рис. 3 квантовой ямы и рис.20 схематического изображения квантовой ямы). Вследствие симметрии отражения относительно центральной плоскости, являющейся центром слоя B,решение уравнения (13) должно быть четным или нечетным по отношению к отражению в этой плоскости. Четности также указаны на рисунке. Благодаря такому выбору ф(r) граничные условия достаточно применить на одном из интерфейсов. Условия на другом будут удовлетворяться автоматически.

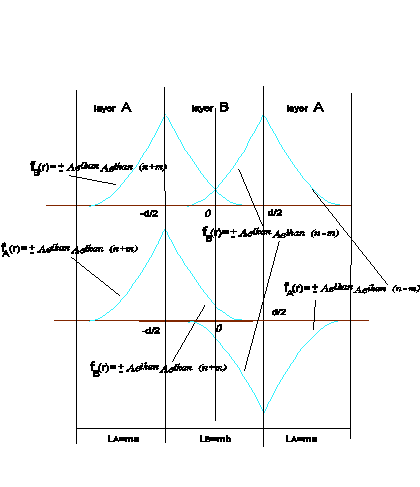
Рис. 20. Схематическое изображение одиночной квантовой ямы В с барьерами из материала А. Показаны волновые функции (сплошные кривые), соответствующие четному (знак +) и нечетному (знак —) потенциалу интерфейсных мод

Итак, для интерфейса АВ в левой части рис. 20 находим

А = B[l ± e^–qxd], Аεе_А(ω) = –Вε_B(ω)[1 ± e^–qxd] (17)

Соответствующее секулярное уравнение приводит к двум ветвям:

ε_A(ω) =–ε_B(ω) th(q_xd)

ε_A(ω) =–ε_B(ω) ch(q_xd) .

Электростатические моды в периодической квантовай яме, т.е. в сверхрешетке, состоящей из слоев материала А с толщиной d_A и материала В с толщиной d_B, можно получить при наложении на потенциал ф{х, z) блоховского условия, связанное с периодичностью сверхрешетки. Используя граничные условия (для Е_||и D_┴) на каждом из интерфейсов АВ и ВА, можно получить типичное секулярное уравнение :

,

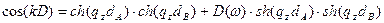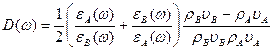. (18)

Уравнение (18) позволяет вычислить зависимость величины блоховского волнового вектора k в сверхрешетке (вдоль направления роста) от ω и q_x. Интересно, что уравнение (18) появилось в результате применения электростатических граничных условий и не гарантирует выполнения механических граничных условий. Оказывается, это приводит к интерфейсным волнам, имеющим не нулевые смещения на границе двух сред. Полезно рассмотреть несколько предельных случаев (18), и прежде всего, случай распространения в плоскости при k = 0, но q_x ≠ 0. Можно показать, что (18) сводится к двум ветвям

–ε_A(ω)/ε_B(ω)= th(q_xd_A/2) ch(q_xd_B/2) либо

–ε_A(ω)/ε_B(ω)= th(q_xd_B/2) ch(q_xd_A/2) .

В случае, когда величина суммарного волнового вектора (q_x + k²)^1/2 стремится к нулю, секулярное уравнение (18) сводится к виду

<ε(ω)><ε^–1(ω)> = tg²θ , (19)

где < > обозначают среднее значение функций на одном периоде сверхрешетки, а θ – угол между волновым вектором и осью роста решетки. Можно установить, что даже при (q_x, k) →0 частота имеет дисперсию, являясь функцией угла θ. Последнее связано с сингулярной природой кулоновского взаимодействия.

В случае распространения волны в плоскости сверхрешетки (т.е. когда угол θ=π/2) уравнение (19) распадается на два уравнения следующего вида:

<ε(ω)>=1/d_AB[d_Aε_A(ω)+ d_Bε_B(ω)]=0 (20a)

<ε^–1(ω)> = 1/d_AB[d_{A /} ε_A(ω)+ d_{B /} ε_B(ω)]=0 . (20b)

Две резонансных частоты в случае стремящегося к нулю волнового вектора при θ=π/2 становятся равными частотам интерфейсных фононов в случае одного интерфейса. При d_A ≠ d_B вырожденные частоты расщепляются.

Уравнения (20 а, б), справедливые при θ=π/2, можно непосредственно получить, применив граничные условия для E_|| и D_┴при k_х →0 (т.е. бесконечной длине волны вдоль х). В этом случае с помощью ф(х, z), приведенного на рис. 20 для слоя В, можно увидеть, что Е_х однородно для четных решений, a E_z — для нечетных. Для первого случая из граничного условия для Е_||:

E_||A= E_||B (21)

и после усреднения по А и В (по периоду) находим:

<D_||A> = <ε(ω)>D_||B (22)

Поэтому периодическую сверхрешетку можно рассматривать как кристалл, имеющий эффективную диэлектрическую функцию <ε(ω)>. «Продольные» моды эффективной среды имеют частоту, определенную выражением (20а). В «нечетном» случае Е_┴однородна, а непрерывность D_┴приводит к уравнению

E_┴ = <1/ ε(ω)> D_┴ (23)

Соответствующую частоту действительно можно найти из (20б). На основании всего изложенного можно рассматривать сверхрешетку как кристалл, в котором объемная симметрия составляющих его сред понижена вседствие слоистости структуры: для системы GaAs/AlAs, выращенной вдоль (001), кубическая точечная группа Т_d понижается до тетрагональной группы D_2d.Таким образом, можно ожидать, что поперечный эффек­тивный заряд е* электронов, определяющий диэлектрическую постоянную среды будет анизотропным, т.е. с разными значениями вдоль направлений [001] и [100]. Поэтому и величина LO-TO зависит от угла θ между вектором распространения волны и осью [001], так что расщепления для θ=π/2 всегда меньше, чем для θ=0.

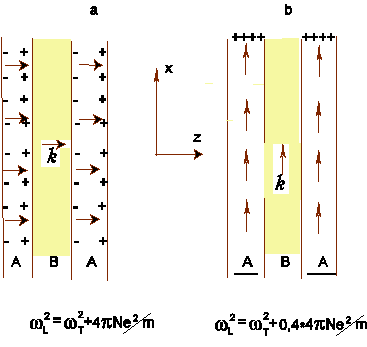
Рис. 21. Схема, иллюстрирующая влияние электростатических эффектов нга фононы, распространяющиеся a) – вдоль и b) – перпендикулярно оси сверхструктуры для мод А-типа.

Рисунок 21 дает простое качественное объяснение данному факту. На рис. 21а эффект деполяризующего поля, приводящий к LO-TO расщеплению, равному расщеплению в объеме, иллюстрируется для распространения вдоль z. На рис. 21b изображен случай распространения LO мод вдоль х. Мы видим, что деполяризующие поля генерируются в слое А для А-подобных мод, но не генерируются в слое В. Вследствие этого деполяризующее поле и сопутствуещее ему LO-TO расщепление становятся меньше.

Приведенная выше картина угловой дисперсии LO-TO расщеплений, подобная той, которая наблюдается в обычных не кубических полярных кристаллах, позволяет сделать еще несколько очевидных выводов. «Интерфейсные» эффекты должны иметь место только для мод, активных в инфракрасной области. В обозначениях выражения (10) эти моды соответствуют нечетным значениям т:для четных мод смещения, а следовательно, и индуцированные дипольные моменты (т.е. средние эффективные заряды), в результате усреднения по одному слою становятся равными нулю. Самые большие эффективные заряды (примерно равные объемным) получаются для т = 1. Для нечетных т ≥ 3 эффективный заряд уменьшается в 1/т раз, а соответствующее LO-TO расщепление — в 1/т ² раз. Поэтому ожидается, что для т ≥ 3 эффекты, связанные с «интерфейсными модами», будут малы.

Вернемся, наконец, к вопросу о том, как можно обосновать пренебрежение механи­ческими граничными условиями, и о возможных последствиях этого пренебрежения. Для θ=π/2 и q_x→0 четная мода на рис. 20 приводит к постоянным значениям ф(r)и и_х внутри слоя В (LO-подобная мода). Для нечетной моды постоянно u_z (ТО-подобная мода). Поскольку для В-подобных мод атомное смещение и в слое А должно быть равно нулю, мы сталкиваемся с принципиальным нарушением непрерывности смещений и при пересечении интерфейсов.

Необходимо сказать, что микроскопические расчеты показывают, что внутри слоя смещения u почти постоянны для интерфейсных мод с m = 1, а вблизи интерфейса стремится к нулю (рис. 22, кривая 2).

Рис. 22. 1 – Огибающая функция для квантованной TOi моды (т.е. 0 = 0) сверхрешетки (GaAs)₆/(AlAs)₆ с осью роста вдоль направления [111]. 2 – Эквивалентные моды для θ=π/2 сплоской вершиной, характерной для интерфейсных мод. (Несмотря на название, эти моды не локализованы около интерфейсов вследствие бесконечной малости q_x. Однако они ближе прижаты к интерфейсам, чем квантованные моды. 3 и 4 – огибающие функции при θ=π/2 для LO-подобных IF мод и мод с m=3. Видно, что их можно разложить на смесь моды типа 2 с плоской вершиной и квантованной моды с m = 3.

При непрерывном изменении θ от 0 до π/2 длинноволновые моды с m = 1 из выражения (10) становятся главными интерфейсными модами, а огибающая функция вместо синусоидальной формы, приведенной на рис. 16, приобретает форму с плоским верхом, характерную для ИФ мод (см. рис. 22, крисая 2). Такая эволюция связана с дальнодействующими электростатически­ми полями. Поэтому интерфейсные IF моды будут вследствие граничных условий смешиваться со всеми ИК-активными квантованными модами с т = 3, 5, 7, ... В результате смеши­вания в дисперсионных зависимостях будут возникать слоожнгые моды, показанные на кривых 3 и 4 на рис. 22.