Модель упругого континуума

Континуальное приближение является подходом феноменологическим, так как в его рамках колебательная система рассматривается в виде упругого континуума. Так же как если рассматривать собственные колебания в струне, которые являются синусоидальными стоячими волнами, как и в плоской круглой пластине, где собственные колебания описываются функциями Бесселя с двумя квантовыми числами, так и колебание сферической частицы можно аппроксимировать колебаниями упругой сферы с тремя квантовыми числами.

Уравнение колебаний упругой сферы можно приближенно записать следующим образом:

.

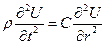Здесь u – смещение, ρ – плотность, С – упругая постоянная среды. Уравнение дает все решения задачи. Их удобно представить в виде функций от скалярного потенциала Ф_sν:

Ф_sν=J_l(kr)P_l^m( cosθ) cosmφ, l=0,1,2,3…, m=–l…0…+1.

Здесь J_l(kr)–сферические функции Бесселя, P_l^m – полиномы Лежандра.

В результате получаются следующие виды решений:

1 L : grad | Φ_n,l,m | ,

2 T₁ : rot [r/R Φ_n,l,m ] ,

3 T₂ : R/ξ rot [rot |r/R Φ_n,l,m |]

4 S : grad [(r/R)^l Y_l,m],

где n, l, m – квантовые числа, R – радиус сферы.

Полное решение колебательного уравнения приводит к существованию трех типов волн. Одно решение L соответствует продольному колебанию. Для таких волн поле смещений является потенциальным, т.е. для вектора смещения divu_LA ≠0. Два других решения T₁и T₂ описывают поперечные волны. Для них divu_TA =0, т.е поле поперечных волн является вихревым. Решение S соответствует поверхностным колебаниям, в которых амплитуда движений убывает по мере приближения к центру сферы. Решение задачи представляется через сферические функции Y_lⁿ , где l, n – квантовые числа. Некоторые из типов продольных волн с квантовыми числами n и l показаны на рис. 28.

22 11

Рис. 28. Некоторые типы колебаний упругой сферы с разными квантовыми числами (l и n)

Задача о собственных колебаниях однородного упругого тела сферической формы со свободной границей впервые была поставлена и решена Лэмбом еще в прошлом веке. Лэмб получил, что основная мода колебаний сферы, соответствующая полносимметричному колебанию, соответствующему попеременному сжатию и расширению сферы, имеет частоту, которая определяется упругой постоянной среды С₁₁, плотностью среды ρ и радиусом сферы R .

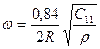или .

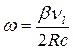Во втором выражении с – скорость света, ν_l – продольная скорость звука, β – коэффициент, зависящий от соотношений продольной и поперечной скорости звука в полупроводнике.

Любопытно, что континуальное приближение (приближение упругого континуума) дает разумные значения частот основной моды даже для микроскопических размеров сферы. Так, стальной «шарик» диаметром 30Ǻ имеет частоту полносимметричной моды 12 см^–1. Такое высокочастотное колебание попадает в далекую инфракрасную область спектра и может наблюдаться в рамановском рассеянии света. Это – так называемая Лэмбовская мода.

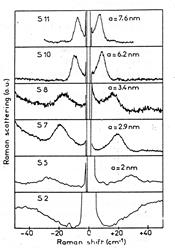
Рис. 29. Стоксовое и антистоксовое низкочастотное рамановское рассеяние для стекол, содержащих CdS_xSe_1-x нанокристаллов с разными радиусами a, указанными на рисунке.

Из рис. 29 видно, что по мере роста размеров нанокристалла происходит сдвиг низкочастотного пика к рэлеевской линии. Эти данные хорошо соответствуют формуле. Рост интенсивности наблюдаемой низкочастотной особенности при увеличении размеров от 20Ǻ до 75Ǻ указывает на повышение концентрации кристаллической фазы в стеклянной матрице.

Кроме низкочастотной области квантово-размерные эффекты проявляются в области оптических колебаний нанокристалла. На рис. 30 представлен экспериментальный спектр рамановского рассеяния нанокристалла смешанных полупроводников CdS_xSe_1-x (при x=0,35) во фторфосфатной стеклообразной матрице

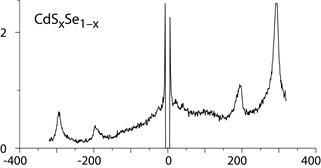
Рис. 30. Экспериментальный спектр нанокристалла смешанного полупроводника CdS_xSe_1-x при x=0.40 в матрице стекла при возбуждающей линии λ=514.5 нм.

Поскольку смешанные кристаллы CdS_xSe_1-x обнаруживают двухмодовое поведение, в спектре КР в области фундаментальных колебаний наблюдаются одновременно две линии, частоты которых близки к частотам чистых соединений вблизи 200 см^–1 и 300 см^–1и соответствующие продольным частотам объемного кристалла.

Из этого рисунка и из рис. 31, где приведены большое количество экспериментальных спектров этих пеолупроводников, хорошо видна большая ширина и асимметричность контуров наблюдаемых линий. Это связано с тем, что в идеальном объемном кристалле в комбинационном рассеянии могут участвовать только фононы с волновым вектором k=0 (центр зоны Бриллюэна), а в нанокристалле, где фононы пространственно ограничены малым объемом периодической структуры, существует неопределенность в значении волнового вектора k, и в спектре КР могут проявляться фононы со всех точек зоны бриллюэна. Конкретизация модели пространственной локализации фонона позволяет определить те моды, которые ответственны за конфайнментное состояние фонона в нанообъекте, и вычислить их мощность.

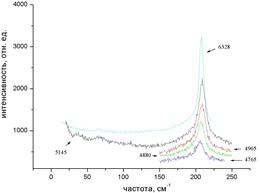
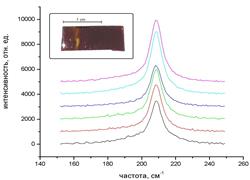
Рис. 31. Спектры КР, полученные для одного из образцов при возбуждении различными длинами волн аргонового лазера и из различных областей образца, показанного на врезке
Цифрами указаны длины волн в ангстремах.