Модель механического континуума

В модели механического континуума предполагается ограничение механического смещения атомов вблизи интерфейса. В работе Рихтера предложена следующая модель пространственного ограничения фононов,смысл которой понятен из рис. 32.

Волновая функция фонона с волновым вектором q₀ в бесконечном кристалле имеет вид функции Блоха:

ф(q_o,r)=u(q_o,r) exp i (q_o,r),

где u(q_o,r) имеет периодичность решётки.

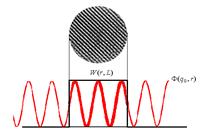
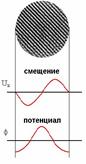
Рис. 32. Схематическое изображение локализованного фонона и граничных условий для смещений u(r)и потенциала ф(r) в модели механического континуума .

.

Если фонон ограничен сферой диаметра R, волновую функцию фонона можно представить в виде

Ψ (q_o,r)=W (r,R)ф(q_o,r) = Ψ´ (q_o,r) u(q_o,r) , Ψ´ (q_o,r)=W (r,R) exp i (q_o,r),

где функция W (r,R) описывает конфайнмент и может быть выбрана различными способами. Волновую функцию Ψ´ (q_o,r) ограниченного фонона можно выразить через интеграл Фурье

Ψ´ (q_o,r)=∫ C(q_o,q) exp i (q_o,r) d³q,

где Фурье-коэффициенты C(q_o,q) даются обратным преобразованием Фурье, т. е. выражением

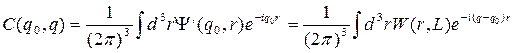
Таким образом, волновая функция ограниченного фонона является результатом суперпозиции плоских волн с волновыми векторами q вблизи q₀. Следовательно, в колебательном спектре должны присутствовать частоты с различными волновыми векторами, а спектральная линия будет образована суперпозицией гармоник. Для описания каждой гармоники удобнее всего взять лоренцево распределение, так как это наиболее простой и удобный способ, позволяющий учесть затухание фонона. Тогда форма линии, наблюдаемой в спектре комбинационного рассеяния, будет складываться из лоренцианов с центрами на частотах w(q) с весовыми множителями, которые задаются типом локализации фонона:

,

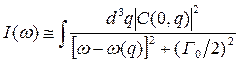где w(q) – дисперсионная зависимость фонона, Г₀ – действительная ширина линии, а интегрирование ведётся по всей зоне Бриллюэна. Имеются физические предпосылки для использования в качестве аподизирующей функции использовать гауссиан, так как он в какой то мере отражает распределение наночастиц по размерам. В таком случае для гауссова распределения W (r,R) = exp[– (ar²/R²)], получаем │C(0,q)│²= exp[– (q²R²/4)], (значение коэффициента a = 4π² получено при анализе контуров рамановских линий для ряда нанокристаллических полупроводников). Тогда в приближении сферической зоны Бриллюэна

.

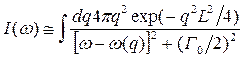Множитель 4pq²появляется после интегрирования по углам, т. е. является следствием приближения сферической зоны Бриллюэна. Построение спектральной линии, а также вклад отдельных гармоник помогает понять рис. 33.

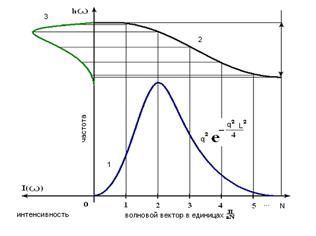
Рис. 33. Вклад внутризонных колебательных мод в спектральную линию колебаний нанокристалла. Данный рисунок состоит из двух зависимостей, объединенных по оси частот. Первая из них (в левой части) образована горизонтальной шкалой интенсивностей и вертикальной школой частот; на ней изображена спектральная линия – результат суммирования отдельных мод в соответствии с весами. Спектральная линия образована суперпозицией отдельных гармоник, суммирование которых производится в соответствии с весовыми множителями. Вторая часть рисунка образована горизонтальной шкалой волновых векторов и общей вертикальной шкалой частот. На ней построена весовая функция, позволяющая увидеть вклад каждой гармоники, и дисперсионная зависимость оптической ветви. На рисунке под цифрой 1 показана зависимость, стоящая в числителе подынтегрального выражения и определяющая мощность отдельных гармоник, т. е. является огибающей весовых множителей. Под цифрой 2 изображена дисперсионная зависимость ω=ω₀+ω/2cos[(π/aN)pa], оптической фононной ветви с шириной 2ω, которая является следствием модели, выбранной для описания колебаний. Вертикальные линии соответствуют дискретным значениям волнового вектора q=(π/aN)p, горизонтальные – возможным частотам колебаний.

В случае кристалла малых размеров волновой вектор принимает ряд дискретных значений, и интеграл заменяется суммой. В колебательном спектре можно ожидать ряд линий на дискретных частотах, определяемых дисперсией соответствующей оптической ветви. Вид спектральной линии в этом случае зависит от размеров нанокристалла. На рис. 34 показана зависимость формы линии отразмеров нанокристалла и величины затухания для одномерной модели (цепочка атомов).

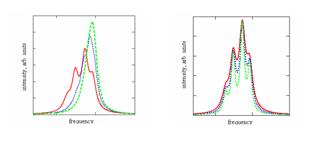
Рис. 34. Контур спектральной линии в зависимости от размеров модели нанокристалла (слева) и величины затухания ω₀.(справа) Размеры цепочки варьируются от 5-ти элементарных ячеек (сплошная линия) до 9 (прерывистая линия), т. е. N=5,7,9. При этом величина затухания составляет ω₀ =5 см^–1. Величина затухания (правый рисунок) принимает значения от ω₀=3см^–1(прерывистая линия) до ω₀=5см^–1 (сплошная линия), т. е. ω ₀ = 3,4,5 см^–1. В этом случае размер цепочки составляет 5 элементарных ячеек.