Рамановское рассеяние на интерфейсных модах
Для наблюдения интерфейсных мод с помощью рамановской спектроскопии волновой вектор рассеянного света должен иметь компоненту в плоскости структуры, так чтобы выполнялось условие θ>0. Однако, впервые интерфейсные моды наблюдались в геометрии рассеяния назад вдоль направления z. При этом необходимый волновой вектор в плоскости структуры возникал вследствие шероховатостей на индивидуальных интерфейсах (благодаря которым в плоскости нарушалась трансляционная инвариантность). На рис. 23 приведены спектры комбинационного рассеяния для AlAs-подобных мод в сверхрешетке GaAs/AlAs. Широкая полоса, расположенная посередине между частотами LO и ТО фононов, характерна для интерфейсных мод в симметричных структурах (т.е. при dA= dB). Наблюдаемыйпик соответствует соотношению εA (ωIF)= –εB (ωIF). В асимметричном случае для получения длинноволновых решений при θ=π/2 следует использовать выражения (26) и (27). В отличие от симметричного случая, при dA≠dB появляются две различных моды. Им отвечают две полосы в спектрах, приведенных в нижней части рис. 23. Доминирует полоса с большим или с меньшим рамановским сдвигом в зависимости от условия dA>dB или dA< dB .
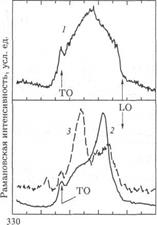
Рис. 23. Рамановские спектры в области частот оптических фононов объемного AlAs, полученные в резонансных условиях при ёь || es для СР GaAs/AlAs (А/В) с различными отношениями между толщиной слоев: 1) йд = с/в; 2) ds — Зс/д; 3) d\ = 3ds при Т = 10 К
Спектры на рис. 23 можно качественно объяснить как проявление простых электростатических интерфейсных мод типа, предсказанного уравнением (18), без учета взаимодействия с квантованными модами с нечетными значениями m.
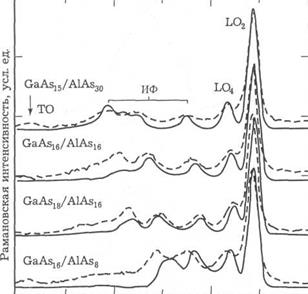
Рис. 24. Сравнение расчетных (сплошные кривые) и измеренных (пунктир) рамановских спектров, обусловленных GaAs-подобными оптическими модами в МКЯ GaAs/AlAs с различной толщиной слоев, в условиях выходного резонанса с переходами el-lhl при 10 К и параллельными поляризациями падающего и рассеянного света. Спектры нормализованы к одинаковой высоте и для наглядности сдвинуты вертикально друг относительно друга.
Проявление полярных колебаний в спектрах комбинационного рассеяния связано в первую очередь с электон-фононым взаимодействием, описываемым фрелиховским потенциалом. Гамильтониан фрёлиховского взаимодействия может быть выражен в виде скалярного электростатического потенциала, умноженного на заряд электрона. Теоретически этот потенциал можно вычислить, используя микроскопические динамические модели решетки с подходящими граничными условиями. Однако, на практике подобные расчеты занимают очень много времени, а получаемые результаты будут справедливы только для заданных в расчете ширин ямы и барьера. Поэтому желательно найти простые, хотя и приближенные, выражения для скалярного потенциала, которые можно было бы использовать для образцов с различной шириной ям. Было предложено несколько таких моделей. Они называются «макроскопическими», поскольку на начальном этапе в них предполагается, что образец представляет собой континуум. Основное различие между этими моделями заключается в подходе к граничным условиям, которые накладываются на оптические фононы на интерфейсах в квантовых ямах или сверхрешетках. В зависимости от применяемых граничных условий одни из них получили название «механических моделей», а другие — «диэлектрических континуальных моделей».
Грубо говоря, в «механических моделях» выдвигается требование, чтобы смещения квантованных LO фононов обращались в нуль на интерфейсе, даже если это приводит к нарушению на нем уравнений Максвелла. Пример картины смещений и электростатического потенциала квантованных LO-фононов, удовлетворяющей механическим граничным условиям, был приведен на рис. 17. Из рисунка видно, что электростатический потенциал ф не исчезает на интерфейсе. Для фонона, квантованного в среде А и обладающего не равным нулю волновым вектром qx, можно представить скалярный потенциал как
ф(х, z)= фоехр (iqxx) cos (кmz)для четного т,
ф(х, z)= фоехр (iqxx) sin (кmz)для нечетного т.
Компонента электрического поля, параллельная интерфейсу {Ех), имеет вид
Ex=–dф/dx=–(iqx) ф(х, z)
и не обращается в нуль на интерфейсе (т.к. потенциал ф на нем не равен нулю), как того требуют условия непрерывности тангенциальных компонент электрического поля на границе двух диэлектрических сред (заметим, что Ех равно нулю в среде В, если имеет место квантовое ограничение фонона в среде А). Поскольку такие модели не учитывают уравнения Максвелла, из них не вытекает существование интерфейсных мод, если не сделаны дополнительные предположения.
В «диэлектрических континуальных моделях», как уже говорилось, в качестве отправной точки используются уравнения Максвелла. На их основании получаются интерфейсные моды как часть решений уравнения Лапласа Ñ 2ф(r)=0. Хотя такие модели и нарушают механические граничные условия (требующие, чтобы атомные смещения квантованных фононов были равны нулю на интерфейсе), однако для интерфейсных мод они являются довольно хорошим приближением к результатам микроскопических вычислений, поскольку в действительности смещения атомов становятся равными нулю только в непосредственной близости от интерфейса.
Макроскопическая модель, в которой предпринята попытка воспроизвести результаты микроскопических вычислений, была предложена Хуаном и Джу. Сделав модельные микроскопические вычисления динамики решетки для определения смещений атомов и электростатического потенциала, они обратили внимание на то, что диэлектрическая континуальная модель дает довольно хорошее приближение к результатам микроскопического расчета, за исключением нарушения механических граничных условий. Интерфейсные моды особенно хорошо описывались этой моделью. Для одновременного выполнения механических и максвелловских граничных условий необходимо, чтобы как ф, так и его производная dф/dz обращались в нуль на интерфейсе. Хуан и Джу заметили, что этого можно достичь, вычитая подходящую константу из ф с четной симметрией (по отношению к отражению в плоскости, проходящей через центр слоя) или подходящий член, линейный по z, из ф с нечетной симметрией.
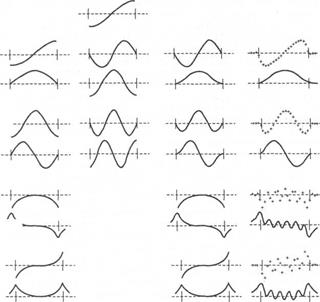
Рис. 25. Сравнение атомных смещений электростатических потенциалов, связанных с самыми низкими квантованными и интерфейсными фононами в GaAs/AlAs, рассчитанных с помощью «макроскопических» моделей: a) диэлектрического континуума; б) механических граничных условий; в) Хуана-Джу; и г) в рамках микроскопической теории.
На рис. 25 потенциалы, связанные с квантованными LO фононами самого низкого порядка и с интерфейсными модами в сверхрешетке GaAs/AlAs, полученные с помощью трех обсуждавшихся выше макроскопических моделей, сравниваются с результатами микроскопической модели. Мы видим, что модель Хуана-Джу является наилучшей аппроксимацией микроскопической модели, за ней следует диэлектрическая континуальная модель. Хотя и существуют различия в вероятностях рассеяния, вычисленных с помощью этих моделей, однако различия между моделью Хуана-Джу и диэлектрической континуальной моделью исчезают в случае ям с малой шириной. Для таких ям основной вклад в вероятность рассеяния вносят интерфейсные моды, а они в этих двух моделях почти идентичны. Полученные в настоящее время экспериментальные результаты лучше всего согласуются с предсказаниями модели Хуана-Джу.
Модель диэлектрического континуума для предельных фононов с k=0
Сравнение с экспериментом требует, как известно, рассмотрения исключительно центрозонных фононов, что соответствует синфазным колебаниям атомов в каждой элементарной ячейке. Поэтому важным является рассмотрение состояния сверхрешетки с однородной поляризацией в каждом слое. Именно такие состояния соответствуют атомным смещениям вдоль собственных векторов центрозонных фононов, и именно такие состояния имеет смысл рассматривать, когда речь идет о возбуждениях, проявляющихся в эксперименте (например, в комбинационном рассеянии). Соответствующую задачу можно рассмотреть в приближении диэлектрического континуума. В рамках такого подхода пренебрегают микроскопическими деталями кристаллической структуры и рассматривают вещество, из которого состоят слои сверхрешетки, как однородную упругую среду с заданной диэлектрической проницаемостью. Это модель, где использованы формулы, выведенные много раньше С. М. Рытовым [ЖЭТФ, 29, N5, 605 (1955)] при решении задачи о распространении радиоволн в слоистой среде. Рассмотрим полярные колебания упругого диэлектрического континуума в бесконечной среде, состоящей из плоских слоев толщины dA и dB с диэлектрической проницаемостью εA и εB периодически повторяющихся в направлении z, перпендикулярном границам раздела. Решая совместно уравнения движения и уравнения Максвелла, и усредняя полученные зависимости по объему, можно получить следующие выражения для эффективной диэлектрической постоянной в плоскости решетки εx,y и перпендикулярно к ней εz:
 , (24)
, (24)
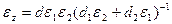 , (25)
, (25)
где  .
.
Полученный результат можно пояснить следующим образом. Электрическое поле в слоях описывается векторами EA и EB и векторами индукции DA= εAEA и DB= εBEB. В случае поля, направленного параллельно оси x, из уравнения rotE=0 следует напряженности поля на границах раздела
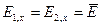 .
.
И, следовательно, среднее значение индукции будет определяться выражением:
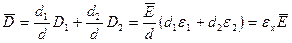 ,
,
из которого непосредственно следует выражение (24).
В случае поля, направленного параллельно оси z, из уравнения divD=0 следует непрерывность индукции на границах раздела
 .
.
И, следовательно, среднее значение напряженности будет определяться выражением:
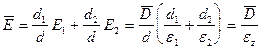 ,
,
из которого непосредственно следует выражение (25).
Выражение (24) соответствует случаю длинноволновых колебаний с поляризацией, перпендикулярно оси z, т.е. колебаниям типа E, а выражение (25) соответствует случаю длинноволновых колебаний с поляризацией, параллельной оси z, т.е. колебаниям типа А. Решение уравнения ε(ω)=0 соответствует LO модам, а частоты, при которых εz(ω) обращается в бесконечность, соответствуют TO модам.
Из формулы (25) непосредственно следует вывод:
εz(ω) → εA(ω)=0 или εB(ω)=0
Это означает, что частоты колебаний A(LО) в СР, совпадают с частотами колебаний A(LО), локализованных в слое A или B. Иными словами, спектр колебаний A(LO) в сверхрешетке состоит из двух мод, частоты которых совпадают с частотами A(LО) мод в объемной структуре.
С другой стороны, из формулы (24) следует,
Εxy(ω) → εA(ω)=∞ или εB(ω)=∞.
Это означает, что частота колебаний E(TO) в сверхрешетке совпадает с частотами таких колебаний, локализованных в каждом из слоев. Иными словами, в сверхрешетке спектр колебаний Е(ТО) состоит из двух мод, частоты которых совпадают с частотами колебаний Е(ТО) в объемном материале.
Таким образом, из уравнений (24 и 25), описывающих волны поляризации в слоистой среде, следует важный вывод: в сверхрешетках существуют длинноволновые оптически активные колебания, частоты которых совпадают с частотами A(LO) и Е(ТО) чистых кристаллов. Собственные векторы этих колебаний включают атомные смещения, локализованные в соответствующих слоях. Иными словами, в сверхрешетках моды A(LO) и Е(ТО) локализованы в отдельных слоях (confined modes) и не зависят от конкретной структуры сверхрешетки (относительной толщины слоев, например).
Иной характер имеют решения уравнений εxy(ω)=0 и εz(ω)=∞ которые соответствуют модам А(ТО) и Е(LO). Для колебаний Е(LO) из соотношения (24) непосредственно следует:
 , (26)
, (26)
а для колебаний A(TO) из соотношения (2) непосредственно следует:
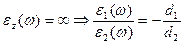 . (27)
. (27)
Зависимость εz(ω) для каждой ОС описывается зависимостью
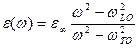 (28),
(28),
причем, компоненты εxy(ω) определяются вкладом Е-мод, а εz(ω) определяются вкладом A-мод. Пользуясь этими соотношениями и решая уравнения (26 и 27) относительно ε(ω), можно вывести выражение для частот A(TO) и E(LO) в сверхрешетке через параметры спектра объемных структур и значения толщины слоев. Вместо вывода этих громоздких выражений, рассмотрим качественно характер зависимости этих решений от отношения dA/dB. Прежде всего заметим, что отношение εA(ω)/εB(ω) (см. рис. 19) принимает отрицательные значения в интервалах ТО1<ω<ТО2 и LO1<ω<LO2. Поскольку в каждом из этих интервалов отношение εA(ω)/εB(ω) монотонно изменяется от нуля до бесконечности, то нетрудно понять, что при любом значении dA/dB каждое из уравнений (26) и (27) имеет по одному решению в этих интервалах. В каждой паре таких решений есть «нормальные» компоненты и «аномальные». Поэтому положение интерфейсных мод болжно зависить от отношения периодов слоев А и В. Это хорошо видно из рис. 26.
По виду кривой, представленной на рис. 26 можно качественно определить характер зависимости частот нормальных и аномальных мод от соотношения толщины слоев в сверхрешетке. Рассмотрим, к примеру, моды A(TO), частоты которых определяются уравнением (4). Нормальное решение этого уравнения из интервала (TO1, TO2) при d1®0 стремится к TO2, а при d2®0 к TO1, т. е. частота этой моды изменяется пропорционально составу сверхрешеки. Аномальное же решение этого уравнения из интервала (LO1, LO2) при d1®0 стремится к LO1, а при d2®0 к LO2, т. е. частота этой моды изменяется обратно пропорционально составу СР. Аналогичные заключения можно вывести и относительно решений E(LO)-I и E(LO)-II.
Используя выражения (24 и 25) и зависимости (28), можно определить положение нулей и полюсов функции ε(ω)при произвольном направлении волнового вектора и, таким образом, исследовать угловую дисперсию нормальных колебаний сверхрешетке.
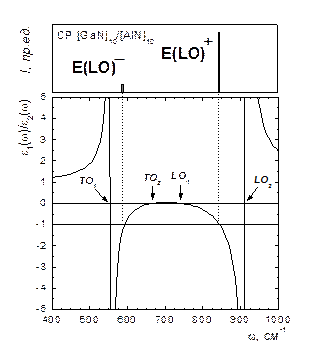
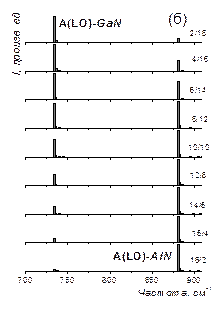
 Рис. 26. Частотная зависимость отношения диэлектрических проницаемостей кристаллов GaN и AlN, из которой можно получить частоты интерфейсных мод сверхрешетки GaN/AlN.
Рис. 26. Частотная зависимость отношения диэлектрических проницаемостей кристаллов GaN и AlN, из которой можно получить частоты интерфейсных мод сверхрешетки GaN/AlN.
Рис. 26а. Рассчитанные КР-спектры СР (AlN)n/(GaN)m, симметрии E(TO) (а) и A(LO) (б) при разных значениях отношениях n/m, указанных на рисунках.
 | |||
 | |||
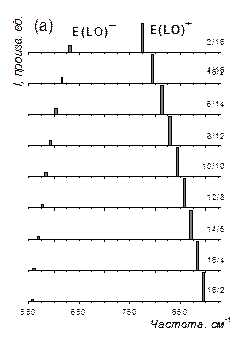
Рис. 26б. Рассчитанные КР-спектры СР (AlN)n/(GaN)m, симметрии E(LO) (а) и A(TO) (б) при разных значениях отношения n/m, указанных на рисунках.
 |
Рис. 26с. Амплитуды смещений атомов в модах A(LO) (а) и E(LO) (б) при различных соотношениях толщины слоев m/n, указанных на рисунке. Значения рассчитанных частот указаны мелкими цифрами.
Дата добавления: 2015-01-29; просмотров: 1268;
