Модель диэлектрического континуума

Для полярных колебаний кристаллов, при которых возникает поляризация среды P и продольное электрическое поле E, уравнения для колебаний нанокристалла можно получить, используя классическую макроскопическую модель с учетом уравнений Максвелла. Такая модель рассматривалась в работе Клейна и была применена для полупроводниковых нанокристаллов CdSe сферической формы. Смысл такой модели понятен из рис. 35. Рассмотрим полупроводниковую сферу радиуса R с диэлектрической постоянной ε, окруженную веществом с диэлектрической проницаемостью ε_d.

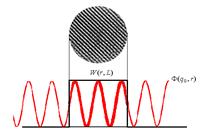
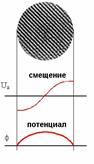
Рис. 35. Схематическое изображение локализованного фонона и граничных условий для смещений u(r)и потенциала ф(r)в модели диэлектрического континуума .

Используем следующие уравнения:

,

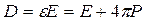
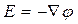
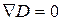где D, E, P, и φ соответственно электрическое смещение, электрическое поле, поляризация и потенциал. Из этих уравнений получаем:

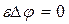
Существуют два типа решений этого уравнения. Первое соответствует ε=0. Для диэлектрической проницаемости можно написать выражение

,

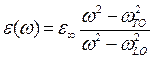где ε_∞ диэлектрическая постоянная при высоких частотах, w_LO и w_TO – собственные частоты, удовлетворяющие соотношению Лиддейна-Сакса-Теллера:

,

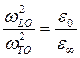где ε₀ – стационарная диэлектрическая постоянная. Случай, когда ε=0 соответствует LO модам собственной частоты w_LO. Собственные функции могущт быть разложены по ортонормированному базису 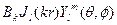, где используются сферические координаты. Здесь 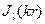сферические функции Бесселя порядка l, 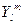-сферические гармоники. Таким образом:

.

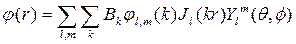Обратное преобразование имеет вид:

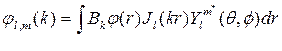
Граничными условиями будут непрерывность φ и нормальной компоненты вектора D на границе раздела, т.е. для LO фононов φ будет уменьшаться до нуля на границе раздела, и вне сферы будет равняться нулю. Возможные решения отвечают таким k, для которых при любых l,m выполнено равенство

J_l(k,R)=0

Эти k зависят от l и определяются соотношениями

k=a_n,l/R

где a_n,l – n-ый нуль сферической функции Бесселя порядка l. Используя выражение J_l(k,R)=0, получаем выражение для константы B_k

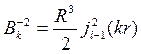
При l=0 она будет равна

,

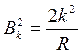где k=nπ/R (n=1,2,3…).

Это рассмотрение в силу нулевых смещений на границе соответствуют случаю механического конфаймента. Решение уравнения εDφ=0, соответствующее e = 0, является наиболее общим описанием механического конфайнмента, где используется разложение потенциала по сферическим гармоникам и нулевые смещения на интерфейсе.

Однако существует и другое решение уравнения εDφ=0, отвечающее условию Df=0. Оно возникает в приближении диэлектрического континуума только для полярных мод, которые вызывают появление макроскопического поля. Данное уравнение дает поверхностные SO (или интерфейсные IF) моды. Возможные решения имеют вид:

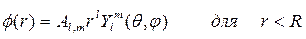
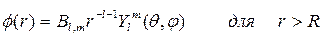
Граничные условия, вытекающие из равенства нормальных составляющих электрического смещения D в двух средах, приводят к соотношению ε grad(φ)=const, и имеют вид:

.

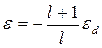Дискретные частоты SO мод в приближении диэлектрического континуума для кристалла CdSe с использованием известных значений e_d, e_∞, w_LO, w_TO приведены в табл.1.

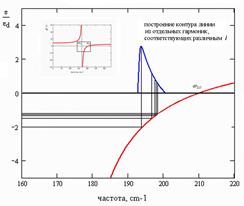
Рис. 36. Схематическое построение контура линии фундаментального колебания нанокристаллов CdSe с использованием модели диэдектрического конфайнмента

Таблица1.

Частоты поверхностных (интерфейсных) мод в нанокристаллах CdSe в стеклянной матрице в cm^–1.

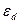
	2.25
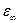
	6.1

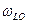
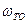
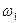
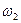
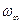
Из таблицы видно, что с изменением l (l=1,2,3…) значения собственных частот SO мод пробегают интервал от 194 до 200 cm^–1.

Значения интерфейсных мод также можно получить, рассматривая как и сверхрешетке среднюю диэлектрическую проницаемость среды, представляющей нанокросталлы полупроводника в стеклянной матрице. Выражение для диэлектрической проницаемости такой структуры легко получить, используя уравнения Рытова для слоевой среды, которые описывают полярные колебания гетероструктуры в приближении диэлектрического континуума. Для бесконечной среды, состоящей из чередующихся слоев толщины d₁ и d₂ с диэлектрической проницаемостью e₁ и e₂, решения этих уравнений приводит к следующим выражениям. Эффективная усредненная диэлектрическая постоянная в плоскости слоев e_x,y и в направлении, перпендикулярном слоям e_z, равна:

e_x,y=d^–1(d₁e₁+d₂e₂)

e_z=de₁e₂(d₁e₂+d₂e₁)^–1,

где d=d₁+d₂.

Для среды, состоящей из сферических нанокристаллов в стекловидной матрице средняя диэлектрическая проницаемость равна:

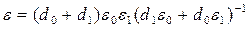
где e₀ ,e₁ – диэлектрические проницаемости матрицы и кристалла, а d₀, d₁– расстояние между кристаллическими включениями и их размер соответственно. Случай, когда диэлектрическая проницаемость среды равна нулю, возможен при равенстве нулю диэлектрических проницаемостей ε₀ или e₁. т. е. соответствует LO модам квантовых точек, так как LO моды матрицы в данной области частот отсутствуют. Диэлектрическая проницаемость равна бесконечности при выполнении условия

,

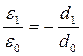что отвечает TO модам, положение которых зависит от d₁/d₀.